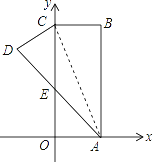
【题目】如图,在直角坐标系中,长方形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(2,6),将长方形沿对角线AC翻折,点B落在点D的位置,且AD交y轴于点E,则点D的坐标为________.
参考答案:
【答案】(﹣![]() ,
,![]() )
)
【解析】
过D作DF⊥AF于F,根据折叠可以证明△CDE≌△AOE,然后利用全等三角形的性质得到OE=DE,OA=CD=2,设OE=x,那么CE=6-x,DE=x,利用勾股定理即可求出OE的长度,利用已知条件可以证明△AEO∽△ADF,而AD=AB=6,利用相似三角形的性质求出DF、AF的长度,即可得出结果.
如图,过D作DF⊥AF于F,

∵点B的坐标为(2,6),
∴AO=2,AB=6,
根据折叠可知:CD=AO=2,
在△CDE和△AOE中,
 ,
,
∴△CDE≌△AOE(AAS),
∴OE=DE,
设OE=x,则CE=6-x,DE=x,
∴在Rt△DCE中,CE2=DE2+CD2,
∴(6-x)2=x2+22,
∴x=![]() ,
,
又∵DF⊥AF,
∴DF∥EO,
∴△AEO∽△ADF,
∵AD=AB=6,
∴AE=CE=6-![]() =
=![]() ,
,
∴![]() ,即
,即![]() ,
,
得:DF=![]() ,AF=
,AF=![]()
∴OF=![]() -2=
-2=![]() ,
,
∴D的坐标为(-![]() ,
,![]() );
);
故答案为:(-![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x,y 的二元一次方程组
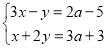 的解都是正数.
的解都是正数. (1)求a的取值范围;
(2)化简:
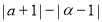 ;
; (3)若上述二元一次方程组的解是一个等腰三角形的一条腰和底边的长,且这个等腰三角形的周长为12,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,电子蚂蚁P、Q在边长为1个单位长度的正方形ABCD的边上运动,电子蚂蚁P从点A出发,以
 个单位长度/秒的速度绕正方形作顺时针运动,电子蚂蚁Q从点A出发,以
个单位长度/秒的速度绕正方形作顺时针运动,电子蚂蚁Q从点A出发,以 个单位长度秒的速度绕正方形作逆时针运动,则它们第2019次相遇在( )
个单位长度秒的速度绕正方形作逆时针运动,则它们第2019次相遇在( )
A. 点AB. 点BC. 点CD. 点D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都为1,在方格纸内将
 经过一次平移后得到
经过一次平移后得到 ,图中标出了点
,图中标出了点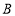 的对应点
的对应点 ,利用网格点和三角板画图或计算:
,利用网格点和三角板画图或计算:
(1)在给定方格纸中画出平移后的
 .
.(2)画出
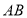 边的中线
边的中线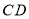 .
.(3)画出
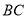 边的高线
边的高线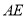 .
.(4)
 的面积为 .
的面积为 .(5)在图中能使
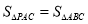 的格点
的格点 的个数有 个 (点
的个数有 个 (点 异于点
异于点 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程组
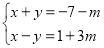 的解满足
的解满足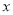 为非正数,
为非正数,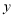 为负数.
为负数.(1)求
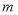 的取值范围
的取值范围(2)在(1)的条件下,若不等式
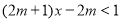 的解为
的解为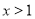 ,求整数
,求整数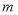 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=
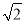 ;将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2,此时AP2=
;将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2,此时AP2=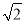 +1;将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时,AP3=
+1;将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时,AP3=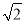 +2…按此规律继续旋转,直至得到点P2026为止,则AP2016= .
+2…按此规律继续旋转,直至得到点P2026为止,则AP2016= .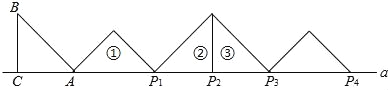
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(2,0),B ( 2,0),C为 y 轴负半轴上一点,D是第四象限内一动点,且始终有BDA 2ACO 成立,过C 点作CE BD 于点 E .
(1)求证:DAC DBC ;
(2)若点 F 在 AD 的延长线上,求证:CD 平分BDF ;

相关试题

