搜索
【题目】如图，在平面直角坐标系内，已知点A（2，2），B（﹣6，﹣4），C（2，﹣4）．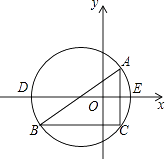 
（1）求△ABC的外接圆的圆心点M的坐标；
（2）求△ABC的外接圆在x轴上所截弦DE的长．
参考答案：
【答案】
（1）解：∵B（﹣6，﹣4），C（2，﹣4），
∴线段BC的垂直平分线是x=﹣2，
∵A（2，2），C（2，﹣4），
∴线段AC的垂直平分线是y=﹣1，
∴△ABC的外接圆的圆心M的坐标为：（﹣2，﹣1）
（2）解：连接OM，作MN⊥DE于N，
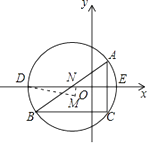
由题意得，AC=6，BC=8，
由勾股定理得，AB=10，
则DN= 
=2 
，
由垂径定理得，DE=2DN=4 ．
【解析】（1）根据三角形的外心是三角形三边垂直平分线的交点解答；（2）连接OM，作MN⊥DE于N，根据勾股定理求出DN，根据垂径定理求出DE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店购进一种商品，每件商品进价30元．试销中发现这种商品每天的销售量y（件）与每件销售价x（元）的关系数据如下：
x
30
32
34
36
y
40
36
32
28
（1）已知y与x满足一次函数关系，根据上表，求出y与x之间的关系式（不写出自变量x的取值范围）；
（2）如果商店销售这种商品，每天要获得150元利润，那么每件商品的销售价应定为多少元？
（3）设该商店每天销售这种商品所获利润为w（元），求出w与x之间的关系式，并求出每件商品销售价定为多少元时利润最大？ -
科目： 来源： 题型：
查看答案和解析>>【题目】“转化”是数学中的一种重要思想，即把陌生的问题转化成熟悉的问题，把复杂的问题转化成简单的问题，把抽象的问题转化为具体的问题．
已知：如图1，线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”，试解答下列问题：
问题一：在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系 ；
问题二：在图2中，若∠D=40°，∠B=36°，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N，试求∠P的度数；
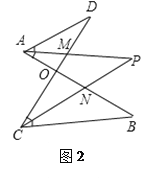
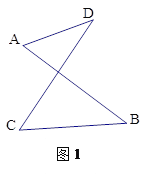
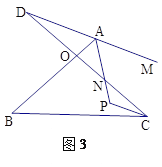
问题三：在图3中，已知AP、CP分别平分∠BAM、∠BCD，请问∠P与∠B、∠D之间存在着怎样的数量关系？并说明理由．
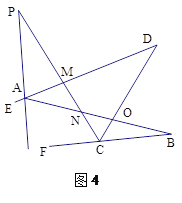
问题四：在图4中，已知AP的反向延长线平分∠EAB，CP平分∠DCF，请直接写出∠P与∠B、∠D之间的数量关系 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】等腰三角形一腰上的高与另一腰的夹角是50
，则这个三角形的底角是( )A. 70
B. 20
C. 70
或20
D. 40
或140
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个挂钟分针针长20 cm，一昼夜它的尖端所走的路程是________cm．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一座桥如图，桥下水面宽度AB是20米，高CD是4米．要使高为3米的船通过，则其宽度须不超过多少米．
（1）如图1，若把桥看做是抛物线的一部分，建立如图坐标系． ①求抛物线的解析式； ②要使高为3米的船通过，则其宽度须不超过多少米？
（2）如图2，若把桥看做是圆的一部分． ①求圆的半径；②要使高为3米的船通过，则其宽度须不超过多少米？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，将一块腰长为
的等腰直角三角板ABC放在第二象限，且斜靠在两坐标轴上，直角顶点C的坐标为（﹣1，0），点B在抛物线y=ax2+ax﹣2上．
（1）点A的坐标为 ， 点B的坐标为；
（2）抛物线的解析式为；
（3）设（2）中抛物线的顶点为D，求△DBC的面积；
（4）在抛物线上是否还存在点P（点B除外），使△ACP仍然是以AC为直角边的等腰直角三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由．
相关试题
