【题目】一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米. 
(1)如图1,若把桥看做是抛物线的一部分,建立如图坐标系. ①求抛物线的解析式; ②要使高为3米的船通过,则其宽度须不超过多少米?
(2)如图2,若把桥看做是圆的一部分. ①求圆的半径;②要使高为3米的船通过,则其宽度须不超过多少米?
参考答案:
【答案】
(1)解:①设抛物线解析式为:y=ax2+c,
∵桥下水面宽度AB是20米,高CD是4米,
∴A(﹣10,0),B(10,0),D(0,4),
∴ ![]() ,
,
解得: 
∴抛物线解析式为:y= ![]() ,
,
②∵要使高为3米的船通过,
∴y=3,则3= ![]() ,
,
解得:x=±5,
∴EF=10米;
(2)解:①设圆半径r米,圆心为W,
∵BW2=BC2+CW2,
∴r2=(r﹣4)2+102,
解得:r=14.5;
②在RT△WGF中,由题可知,WF=14.5,WG=14.5﹣1=13.5,
根据勾股定理知:GF2=WF2﹣WG2,
即GF2=14.52﹣13.52=28,
所以GF=2 ![]() ,
,
此时宽度EF=4 ![]() 米.
米.

【解析】(1)①利用待定系数法求函数解析式即可;②根据题意得出y=3时,求出x的值即可;(2)①构造直角三角形利用BW2=BC2+CW2 , 求出即可;②在RT△WGF中,由题可知,WF=14.5,WG=14.5﹣1=13.5,根据勾股定理知:GF2=WF2﹣WG2 , 求出即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一腰上的高与另一腰的夹角是50
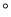 ,则这个三角形的底角是( )
,则这个三角形的底角是( )A. 70
 B. 20
B. 20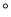 C. 70
C. 70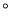 或20
或20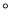 D. 40
D. 40 或140
或140
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系内,已知点A(2,2),B(﹣6,﹣4),C(2,﹣4).
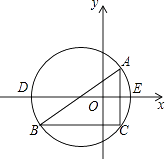
(1)求△ABC的外接圆的圆心点M的坐标;
(2)求△ABC的外接圆在x轴上所截弦DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个挂钟分针针长20 cm,一昼夜它的尖端所走的路程是________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将一块腰长为
 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(﹣1,0),点B在抛物线y=ax2+ax﹣2上.
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(﹣1,0),点B在抛物线y=ax2+ax﹣2上.
(1)点A的坐标为 , 点B的坐标为;
(2)抛物线的解析式为;
(3)设(2)中抛物线的顶点为D,求△DBC的面积;
(4)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图像可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x,
 的方程组
的方程组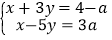 ,给出下列结论:①
,给出下列结论:①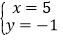 是方程组的解;②无论a取何值, x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④
是方程组的解;②无论a取何值, x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④ ,
,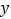 都为自然数的解有4对.其中正确的为______________.
都为自然数的解有4对.其中正确的为______________.
相关试题

