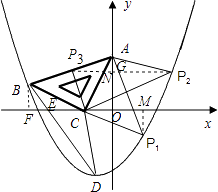
【题目】如图,在平面直角坐标系中,将一块腰长为 ![]() 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(﹣1,0),点B在抛物线y=ax2+ax﹣2上.
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(﹣1,0),点B在抛物线y=ax2+ax﹣2上.
(1)点A的坐标为 , 点B的坐标为;
(2)抛物线的解析式为;
(3)设(2)中抛物线的顶点为D,求△DBC的面积;
(4)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)(0,2);(﹣3,1)
(2)y= ![]() x2+
x2+ ![]() x﹣2
x﹣2
(3)
解:由(2)中抛物线的解析式可知,抛物线的顶点D(﹣ ![]() ,﹣
,﹣ ![]() ),
),
设直线BD的关系式为y=kx+b,将点B、D的坐标代入得:
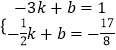 ,
,
解得 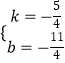 .
.
∴BD的关系式为y=﹣ ![]() x﹣
x﹣ ![]() .
.
设直线BD和x 轴交点为E,则点E(﹣ ![]() ,0),CE=
,0),CE= ![]() .
.
∴S△DBC= ![]() ×
× ![]() ×(1+
×(1+ ![]() )=
)= ![]()
(4)
解:假设存在点P,使得△ACP仍然是以AC为直角边的等腰直角三角形:
①若以点C为直角顶点;
则延长BC至点P1,使得P1C=BC,得到等腰直角三角形△ACP1,
过点P1作P1M⊥x轴,
∵CP1=BC,∠MCP1=∠BCF,∠P1MC=∠BFC=90°,
∴△MP1C≌△FBC.
∴CM=CF=2,P1M=BF=1,
∴P1(1,﹣1);
②若以点A为直角顶点;
i)则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形△ACP2,
过点P2作P2N⊥y轴,同理可证△AP2N≌△CAO,
∴NP2=OA=2,AN=OC=1,
∴P2(2,1),
ii)若以点P为直角顶点.
过P3作P3G⊥y轴于G,
同理,△AGP3≌△CAO,
∴GP3=OA=2,AG=OC=1,
∴P3为(﹣2,3).
经检验,点P1(1,﹣1)与点P2(2,1)都在抛物线y= ![]() x2+
x2+ ![]() x﹣2上,点P3(﹣2,3)不在抛物线上.
x﹣2上,点P3(﹣2,3)不在抛物线上.
故点P的坐标为P1(1,﹣1)与P2(2,1).
【解析】解:(1)∵C(﹣1,0),AC= ![]() ,
,
∴OA= ![]() =
= ![]() =2,
=2,
∴A(0,2);
过点B作BF⊥x轴,垂足为F,
∵∠ACO+∠CAO=90°,∠ACO+∠BCF=90°,∠BCF+∠FBC=90°,
在△AOC与△CFB中,
∵ 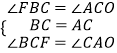 ,
,
∴△AOC≌△CFB,
∴CF=OA=2,BF=OC=1,
∴OF=3,
∴B的坐标为(﹣3,1),
所以答案是:(0,2),(﹣3,1);(2)∵把B(﹣3,1)代入y=ax2+ax﹣2得:
1=9a﹣3a﹣2,
解得a= ![]() ,
,
∴抛物线解析式为:y= ![]() x2+
x2+ ![]() x﹣2.
x﹣2.
所以答案是:y= ![]() x2+
x2+ ![]() x﹣2;
x﹣2;
【考点精析】本题主要考查了等腰直角三角形和二次函数的图象的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系内,已知点A(2,2),B(﹣6,﹣4),C(2,﹣4).
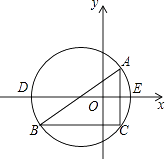
(1)求△ABC的外接圆的圆心点M的坐标;
(2)求△ABC的外接圆在x轴上所截弦DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个挂钟分针针长20 cm,一昼夜它的尖端所走的路程是________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米.

(1)如图1,若把桥看做是抛物线的一部分,建立如图坐标系. ①求抛物线的解析式; ②要使高为3米的船通过,则其宽度须不超过多少米?
(2)如图2,若把桥看做是圆的一部分. ①求圆的半径;②要使高为3米的船通过,则其宽度须不超过多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图像可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x,
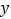 的方程组
的方程组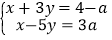 ,给出下列结论:①
,给出下列结论:①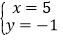 是方程组的解;②无论a取何值, x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④
是方程组的解;②无论a取何值, x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④ ,
,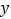 都为自然数的解有4对.其中正确的为______________.
都为自然数的解有4对.其中正确的为______________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三边AB、BC、CA的长分别为40、50、60,其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO等于 ( )
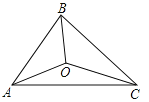
A. 1:2:3 B. 2:3:4 C. 3:4:5 D. 4:5:6
相关试题

