【题目】等腰三角形一腰上的高与另一腰的夹角是50![]() ,则这个三角形的底角是( )
,则这个三角形的底角是( )
A. 70![]() B. 20
B. 20![]() C. 70
C. 70![]() 或20
或20![]() D. 40
D. 40![]() 或140
或140![]()
参考答案:
【答案】C
【解析】分两种情况讨论如下:
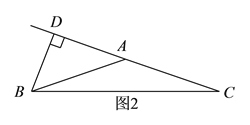
(1)当该等腰三角形是锐角三角形时,如图1,△ABC中,AB=AC,BD⊥AC于点D,∠ABD=50°,求∠C的度数.
∵BD⊥AC于点D,
∴∠ADB=90°,
又∵∠ABD=50°,
∴∠A=90°-50°=40°,
又∵AB=AC,
∴∠C=![]() ;
;
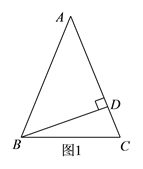
(2)当该等腰三角形是钝角三角形时,如图2,△ABC中,AB=AC,BD⊥AC于点D,∠ABD=50°,求∠C的度数.
∵BD⊥AC于点D,
∴∠ADB=90°,
又∵∠ABD=50°,
∴∠BAD=90°-50°=40°,
∴∠BAC=180°-40°=140°,
又∵AB=AC,
∴∠C=![]() ;
;
综上所述,该等腰三角形的底角为70°或20°.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”是对古丝绸之路的传承和提升,让中国和世界的联系更紧密,电气设备是“一带一路”沿线国家受青睐的商品。某企业计划生产甲、乙两种电气设备出口,甲种设备售价50千元/件,乙种设备售价30千元/件,生产这两种设备需要A、B两种原料,生产甲设备需要A种原料4吨/件,B种原料2吨/件,生产乙设备需要A种原料3吨/件,B种原料1吨/件,已知A种原料有120吨,B种原料有50吨.
(1)如何安排生产,才能恰好使A、B两种原料全部用完?此时总产值是多少千元?
(2)若使甲种设备售价上涨10%,而乙种设备售价下降10%,并且要求甲种设备比乙种设备多生产25件,问如何安排甲、乙两种设备的生产,使销售总产值能达到1375千元,此时A、B两种原料还剩下多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下:
x
30
32
34
36
y
40
36
32
28
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
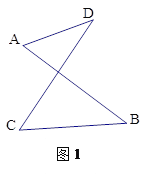
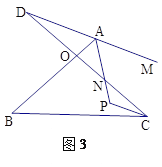
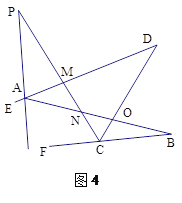
已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”,试解答下列问题:
问题一:在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系 ;
问题二:在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N,试求∠P的度数;
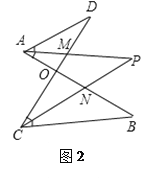
问题三:在图3中,已知AP、CP分别平分∠BAM、∠BCD,请问∠P与∠B、∠D之间存在着怎样的数量关系?并说明理由.
问题四:在图4中,已知AP的反向延长线平分∠EAB,CP平分∠DCF,请直接写出∠P与∠B、∠D之间的数量关系 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系内,已知点A(2,2),B(﹣6,﹣4),C(2,﹣4).
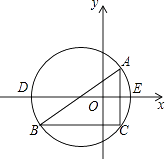
(1)求△ABC的外接圆的圆心点M的坐标;
(2)求△ABC的外接圆在x轴上所截弦DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个挂钟分针针长20 cm,一昼夜它的尖端所走的路程是________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米.

(1)如图1,若把桥看做是抛物线的一部分,建立如图坐标系. ①求抛物线的解析式; ②要使高为3米的船通过,则其宽度须不超过多少米?
(2)如图2,若把桥看做是圆的一部分. ①求圆的半径;②要使高为3米的船通过,则其宽度须不超过多少米?
相关试题

