【题目】已知直线![]() 分别交x轴、y轴于A、B两点,抛物线
分别交x轴、y轴于A、B两点,抛物线![]() 经过点A,和x轴的另一个交点为C.
经过点A,和x轴的另一个交点为C.

![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 如图1,点D是抛物线上的动点,且在第三象限,求
如图1,点D是抛物线上的动点,且在第三象限,求![]() 面积的最大值;
面积的最大值;
![]() 如图2,经过点
如图2,经过点![]() 的直线交抛物线于点P、Q,连接CP、CQ分别交y轴于点E、F,求
的直线交抛物线于点P、Q,连接CP、CQ分别交y轴于点E、F,求![]() 的值.
的值.
备注:抛物线顶点坐标公式![]()
参考答案:
【答案】![]() 抛物线的解析式为
抛物线的解析式为![]() ;
;![]() ;
;![]() .
.
【解析】
![]() 先求得点A的坐标,然后将点A的坐标代入抛物线的解析式求得m的值即可;
先求得点A的坐标,然后将点A的坐标代入抛物线的解析式求得m的值即可;
![]() 过点D作
过点D作![]() 轴,交A与点H,设
轴,交A与点H,设![]() ,
,![]() ,然后用含n的式子表示DH的长,接下来,利用配方法求得DH的最大值,从而可求得
,然后用含n的式子表示DH的长,接下来,利用配方法求得DH的最大值,从而可求得![]() 面积最大值;
面积最大值;
![]() 先求得点C的坐标,然后设直线CQ的解析式为
先求得点C的坐标,然后设直线CQ的解析式为![]() ,CP的解析式为
,CP的解析式为![]() ,接下来求得点Q和点P的横坐标,然后设直线PQ的解析式为
,接下来求得点Q和点P的横坐标,然后设直线PQ的解析式为![]() ,把
,把![]() 代入得:
代入得:![]() ,将PQ的解析式为与抛物线解析式联立得到关于x的一元二次方程,然后依据一元二次方程根与系数的关系可求得
,将PQ的解析式为与抛物线解析式联立得到关于x的一元二次方程,然后依据一元二次方程根与系数的关系可求得![]() ,最后,由ab的值可得到
,最后,由ab的值可得到![]() 的值.
的值.
![]() 把
把![]() 代入
代入![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
![]() ,
,
把点A的坐标代入![]() 得:
得:![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() ;
;
![]() 过点D作
过点D作![]() 轴,交A与点H,
轴,交A与点H,

设![]() ,
,![]() ,
,
![]() ,
,
![]() 当
当![]() 时,DH最大,最大值为
时,DH最大,最大值为![]() ,
,
此时![]() 面积最大,最大值为
面积最大,最大值为![]() ;
;
![]() 把
把![]() 代入
代入![]() ,得:
,得:![]() ,解得:
,解得:![]() 或
或![]() ,
,
![]() ,
,
设直线CQ的解析式为![]() ,CP的解析式为
,CP的解析式为![]() ,
,
 ,解得:
,解得:![]() 或
或![]() ,
,
![]() ,
,
同理:![]() ,
,
设直线PQ的解析式为![]() ,把
,把![]() 代入得:
代入得:![]() ,
,
 ,
,
![]() ,
,
![]() ,
,![]() ,
,
解得:![]() ,
,
又![]() ,
,![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是
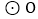 的直径,AC为弦,
的直径,AC为弦,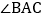 的平分线交
的平分线交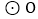 于点D,过点D的切线交AC的延长线于点E.
于点D,过点D的切线交AC的延长线于点E.求证:
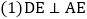 ;
;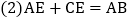 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节期间,甲、乙两人沿同一路线行驶,各自开车同时去离家560千米的景区游玩,甲先以每小时60千米的速度匀速行驶1小时,再以每小时m千米的速度匀速行驶,途中体息了一段时间后,仍按照每小时m千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程
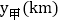 ,
,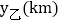 与时间
与时间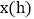 之间的函数关系的图象
之间的函数关系的图象 请根据图象提供的信息,解决下列问题:
请根据图象提供的信息,解决下列问题: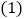 图中E点的坐标是______,题中
图中E点的坐标是______,题中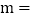 ______
______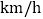 ,甲在途中休息______h;
,甲在途中休息______h; 求线段CD的解析式,并写出自变量x的取值范围;
求线段CD的解析式,并写出自变量x的取值范围;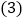 两人第二次相遇后,又经过多长时间两人相距20km?
两人第二次相遇后,又经过多长时间两人相距20km?
-
科目: 来源: 题型:
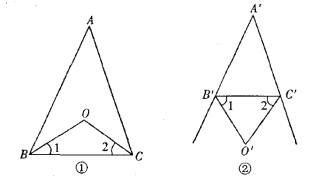
查看答案和解析>>【题目】(1)如图①,在△ABC中,∠ABC、∠ACB的平分线相交于点O,∠A=40°,求∠BOC的度数;
(2)如图②,△A′B′C′的外角平分线相交于点O′,∠A′=40°,求∠B′O′C′的度数;
(3)上面(1)(2)两题中的∠BOC与∠B′O′C′ 有怎样的数量关系?若∠A=∠A′=n°,∠BOC与∠B′O′C′ 是否还具有这样的关系?这个结论你是怎样得到的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备租用一批汽车,现有甲、乙两种客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人.已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.求1辆甲种客车和1辆乙种客车的租金分别是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元)
5
10
20
50
100
人数(单位:个)
2
4
5
3
1
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD的边长为8,点P是边AD的中点,点E是正方形ABCD的边上一点,若
 是等腰三角形,则腰长为______.
是等腰三角形,则腰长为______.
相关试题

