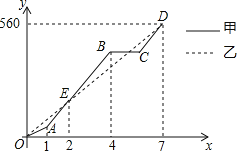
【题目】端午节期间,甲、乙两人沿同一路线行驶,各自开车同时去离家560千米的景区游玩,甲先以每小时60千米的速度匀速行驶1小时,再以每小时m千米的速度匀速行驶,途中体息了一段时间后,仍按照每小时m千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程![]() ,
,![]() 与时间
与时间![]() 之间的函数关系的图象
之间的函数关系的图象![]() 请根据图象提供的信息,解决下列问题:
请根据图象提供的信息,解决下列问题:
![]() 图中E点的坐标是______,题中
图中E点的坐标是______,题中![]() ______
______![]() ,甲在途中休息______h;
,甲在途中休息______h;
![]() 求线段CD的解析式,并写出自变量x的取值范围;
求线段CD的解析式,并写出自变量x的取值范围;
![]() 两人第二次相遇后,又经过多长时间两人相距20km?
两人第二次相遇后,又经过多长时间两人相距20km?
参考答案:
【答案】![]() ,100,1;
,100,1;![]() 直线CD的解析式为:
直线CD的解析式为:![]() ;
;![]() 两人第二次相遇后,又经过
两人第二次相遇后,又经过![]() 时或
时或![]() 时两人相距
时两人相距![]()
【解析】
(1)根据速度和时间列方程:60×1+m=160,可得m=100,根据D的坐标可计算直线OD的解析式,从图中知E的横坐标为2,可得E的坐标,根据点E到D的时间差及速度可得休息的时间;
(2)利用待定系数法求直线CD的解析式;
(3)先计算第二次相遇的时间:y=360时代入y=80x可得x的值,再计算x=5时直线OD的路程,可得路程差为40km,所以存在两种情况:两人相距20km,列方程可得结论.
![]() 由图形得
由图形得![]() ,
,
设OD的解析式为:![]() ,
,
把![]() 代入得:
代入得:![]() ,
,![]() ,
,
![]() :
:![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,
由题意得:![]() ,
,![]() ,
,
![]() ,
,
故答案为:![]() ,100,1;
,100,1;
![]() ,
,![]() ,
,
![]() 直线AE:
直线AE:![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 设CD的解析式为:
设CD的解析式为:![]() ,
,
把![]() ,
,![]() 代入得:
代入得:![]() ,解得:
,解得:![]() ,
,
![]() 直线CD的解析式为:
直线CD的解析式为:![]() ;
;
![]() 的解析式为:
的解析式为:![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() 出发5h时两个相距40km,
出发5h时两个相距40km,
把![]() 代入
代入![]() 得:
得:![]() ,
,
![]() 出发
出发![]() 时两人第二次相遇,
时两人第二次相遇,
![]() 当
当![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,
答:两人第二次相遇后,又经过![]() 时或
时或![]() 时两人相距
时两人相距![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
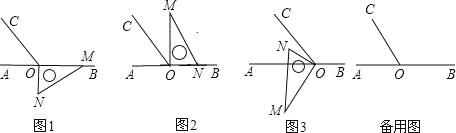
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为 度;
(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转到图3的位置的过程中,若三角板绕点O按15°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在由边长为1的小正方形组成的网格图中有△ABC,建立平面直角坐标系后,点O的坐标是(0,0).
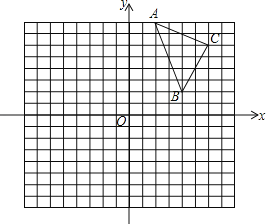
(1)以O为位似中心,作△A′B′C′∽△ABC,相似比为1:2,且保证△A′B′C′在第三象限;
(2)点B′的坐标为( , );
(3)若线段BC上有一点D,它的坐标为(a,b),那么它的对应点D′的坐标为( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
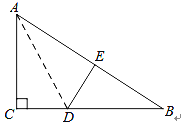
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?
(2)若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;
(3)在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
 .
.(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司开发了一种新产品,现要在甲地或者乙地进行销售,设年销售量为x(件),其中x>0.
若在甲地销售,每件售价y(元)与x之间的函数关系式为y=﹣
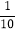 x+100,每件成本为20元,设此时的年销售利润为w甲(元)(利润=销售额﹣成本).
x+100,每件成本为20元,设此时的年销售利润为w甲(元)(利润=销售额﹣成本).若在乙地销售,受各种不确定因素的影响,每件成本为a元(a为常数,18≤a≤25 ),每件售价为98元,销售x(件)每年还需缴纳
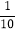 x2元的附加费.设此时的年销售利润为w乙(元)(利润=销售额﹣成本﹣附加费).
x2元的附加费.设此时的年销售利润为w乙(元)(利润=销售额﹣成本﹣附加费).(1)当a=18,且x=100是,w乙= 元;
(2)求w甲与x之间的函数关系式(不必写出x的取值范围),当w甲=15000时,若使销售量最大,求x的值;
(3)为完成x件的年销售任务,请你通过分析帮助公司决策,应选择在甲地还是在乙地销售才能使该公司所获年利润最大.
相关试题

