【题目】正方形ABCD的边长为8,点P是边AD的中点,点E是正方形ABCD的边上一点,若![]() 是等腰三角形,则腰长为______.
是等腰三角形,则腰长为______.
参考答案:
【答案】5或![]() 或
或![]()
【解析】
分情况讨论:![]() 当PB为腰时,若P为顶点,则E点和C点重合,求出PB长度即可;若B为顶点,则E点为CD中点;
当PB为腰时,若P为顶点,则E点和C点重合,求出PB长度即可;若B为顶点,则E点为CD中点;![]() 当PB为底时,E在BP的垂直平分线上,与正方形的边交于两点,即为点E;
当PB为底时,E在BP的垂直平分线上,与正方形的边交于两点,即为点E;
①由题意得出![]() ,证明
,证明![]() ∽
∽![]() ,得出比例式
,得出比例式![]() ,即可求出BE;②设
,即可求出BE;②设![]() ,则
,则![]() ,根据勾股定理得出方程求出CE,再由勾股定理求出BE即可.
,根据勾股定理得出方程求出CE,再由勾股定理求出BE即可.
分情况讨论:![]() 当PB为腰时,若P为顶点,则E点与C点重合,如图1所示:
当PB为腰时,若P为顶点,则E点与C点重合,如图1所示: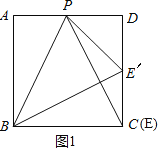
![]() 四边形ABCD是正方形,
四边形ABCD是正方形,![]() ,
,![]() ,
,![]() 是AD的中点,
是AD的中点,![]() ,
,
根据勾股定理得:![]() ;
;
若B为顶点,则根据![]() 得,
得,![]() 为CD中点,此时腰长
为CD中点,此时腰长![]() ;
;![]() 当PB为底边时,E在BP的垂直平分线上,与正方形的边交于两点,即为点E;
当PB为底边时,E在BP的垂直平分线上,与正方形的边交于两点,即为点E;
当E在AB上时,如图2所示:
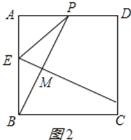
则![]() ,
,![]() ,
,![]() ,
,![]() ∽
∽![]() ,
,![]() ,即
,即![]() ,
,![]() ;
;
②当E在CD上时,如图3所示:
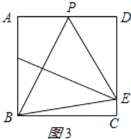
设![]() ,则
,则![]() ,
,
根据勾股定理得:![]() ,
,![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,![]() ;
;
综上所述:腰长为:![]() ,或5,或
,或5,或![]() ;
;
故答案为:![]() ,或5,或
,或5,或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
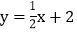 分别交x轴、y轴于A、B两点,抛物线
分别交x轴、y轴于A、B两点,抛物线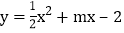 经过点A,和x轴的另一个交点为C.
经过点A,和x轴的另一个交点为C.
 求抛物线的解析式;
求抛物线的解析式; 如图1,点D是抛物线上的动点,且在第三象限,求
如图1,点D是抛物线上的动点,且在第三象限,求 面积的最大值;
面积的最大值; 如图2,经过点
如图2,经过点 的直线交抛物线于点P、Q,连接CP、CQ分别交y轴于点E、F,求
的直线交抛物线于点P、Q,连接CP、CQ分别交y轴于点E、F,求 的值.
的值.备注:抛物线顶点坐标公式

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备租用一批汽车,现有甲、乙两种客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人.已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.求1辆甲种客车和1辆乙种客车的租金分别是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元)
5
10
20
50
100
人数(单位:个)
2
4
5
3
1
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知D,E分别为边BC,AD的中点,且S△ABC=4 cm2,则△BEC的面积为( )

A. 2 cm2 B. 1 cm2 C. 0.5 cm2 D. 0.25 cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )

A.23°B.92°C.44°D.46°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件中,
 ;
; ;
; ;
; ;
; ;
; 。能构成直角三角形的个数有( )个。
。能构成直角三角形的个数有( )个。A.3B.4C.5D.6
相关试题

