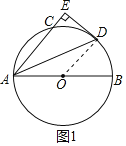
【题目】如图,AB是![]() 的直径,AC为弦,
的直径,AC为弦,![]() 的平分线交
的平分线交![]() 于点D,过点D的切线交AC的延长线于点E.
于点D,过点D的切线交AC的延长线于点E.
求证:![]() ;
;
![]() .
.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)连接OD,根据等腰三角形的性质结合角平分线的性质可得出∠CAD=∠ODA,利用“内错角相等,两直线平行”可得出AE//OD,结合切线的性质即可证出DE⊥AE;
(2)过点D作DM⊥AB于点M,连接CD、DB,根据角平分线的性质可得出DE=DM,结合AD=AD、∠AED=∠AMD=90°即可证出△DAE≌△DAM(SAS),根据全等三角形的性质可得出AE=AM,由∠EAD=∠MAD可得出![]() ,进而可得出CD=BD,结合DE=DM可证出Rt△DEC≌Rt△DMB(HL),根据全等三角形的性质可得出CE=BM,结合AB=AM+BM即可证出AE+CE=AB.
,进而可得出CD=BD,结合DE=DM可证出Rt△DEC≌Rt△DMB(HL),根据全等三角形的性质可得出CE=BM,结合AB=AM+BM即可证出AE+CE=AB.
![]() 连接OD,如图1所示,
连接OD,如图1所示,
![]() ,AD平分
,AD平分![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的切线,
的切线,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 过点D作
过点D作![]() 于点M,连接CD、DB,如图2所示,
于点M,连接CD、DB,如图2所示,

![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,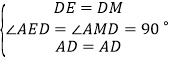 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知两条直线AB,CD被直线EF所截,分别交于点E,点F,EM平分∠AEF交CD于点M,且∠FEM=∠FME.

(1)直线AB与直线CD是否平行,说明你的理由;
(2)如图2,点G是射线MD上一动点(不与点M,F重合),EH平分∠FEG交CD于点H,过点H作HN⊥EM于点N,设∠EHN=α,∠EGF=β.
①当点G在点F的右侧时,若β=60°,求α的度数;
②当点G在运动过程中,α和β之间有怎样的数量关系?请写出你的猜想,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, ,D、E分别是斜边AB、直角边BC上的点,把
,D、E分别是斜边AB、直角边BC上的点,把 沿着直线DE折叠.
沿着直线DE折叠.
 如图1,当折叠后点B和点A重合时,用直尺和圆规作出直线DE;
如图1,当折叠后点B和点A重合时,用直尺和圆规作出直线DE; 不写作法和证明,保留作图痕迹
不写作法和证明,保留作图痕迹
 如图2,当折叠后点B落在AC边上点P处,且四边形PEBD是菱形时,求折痕DE的长.
如图2,当折叠后点B落在AC边上点P处,且四边形PEBD是菱形时,求折痕DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的中线,△ABD的周长比△BCD的周长多2 cm.若△ABC的周长为18 cm,且AC=4 cm,求AB和BC的长..

-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节期间,甲、乙两人沿同一路线行驶,各自开车同时去离家560千米的景区游玩,甲先以每小时60千米的速度匀速行驶1小时,再以每小时m千米的速度匀速行驶,途中体息了一段时间后,仍按照每小时m千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程
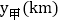 ,
,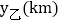 与时间
与时间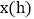 之间的函数关系的图象
之间的函数关系的图象 请根据图象提供的信息,解决下列问题:
请根据图象提供的信息,解决下列问题: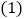 图中E点的坐标是______,题中
图中E点的坐标是______,题中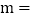 ______
______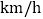 ,甲在途中休息______h;
,甲在途中休息______h; 求线段CD的解析式,并写出自变量x的取值范围;
求线段CD的解析式,并写出自变量x的取值范围; 两人第二次相遇后,又经过多长时间两人相距20km?
两人第二次相遇后,又经过多长时间两人相距20km?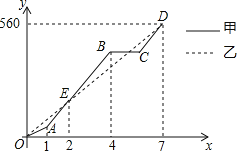
-
科目: 来源: 题型:
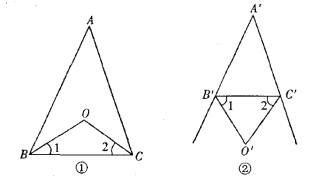
查看答案和解析>>【题目】(1)如图①,在△ABC中,∠ABC、∠ACB的平分线相交于点O,∠A=40°,求∠BOC的度数;
(2)如图②,△A′B′C′的外角平分线相交于点O′,∠A′=40°,求∠B′O′C′的度数;
(3)上面(1)(2)两题中的∠BOC与∠B′O′C′ 有怎样的数量关系?若∠A=∠A′=n°,∠BOC与∠B′O′C′ 是否还具有这样的关系?这个结论你是怎样得到的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
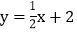 分别交x轴、y轴于A、B两点,抛物线
分别交x轴、y轴于A、B两点,抛物线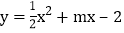 经过点A,和x轴的另一个交点为C.
经过点A,和x轴的另一个交点为C.
 求抛物线的解析式;
求抛物线的解析式; 如图1,点D是抛物线上的动点,且在第三象限,求
如图1,点D是抛物线上的动点,且在第三象限,求 面积的最大值;
面积的最大值; 如图2,经过点
如图2,经过点 的直线交抛物线于点P、Q,连接CP、CQ分别交y轴于点E、F,求
的直线交抛物线于点P、Q,连接CP、CQ分别交y轴于点E、F,求 的值.
的值.备注:抛物线顶点坐标公式

相关试题

