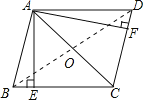
【题目】如图,在ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:ABCD是菱形;
(2)若AB=5,AC=6,求ABCD的面积.

参考答案:
【答案】(1)证明见解析;(2)S平行四边形ABCD =24
【解析】
(1)利用全等三角形的性质证明AB=AD即可解决问题;
(2)连接BD交AC于O,利用勾股定理求出对角线的长即可解决问题;
(1)∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
∵BE=DF,
∴△AEB≌△AFD,
∴AB=AD,
∴四边形ABCD是平行四边形;
(2)连接BD交AC于O,
∵四边形ABCD是菱形,AC=6,
∴AC⊥BD,
AO=OC=![]() AC=
AC=![]() ×6=3,
×6=3,
∵AB=5,AO=3,
∴BO=![]() =
=![]() =4,
=4,
∴BD=2BO=8,
∴S平行四边形ABCD=![]() ×AC×BD=24.
×AC×BD=24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是随机抽取的某公司部分员工的月收入资料.
(1)请计算样本的平均数和中位数;
(2)甲乙两人分别用样本平均数和中位数来估计推断公司全体员工月收入水平,请你写出甲乙两人的推断结论;并指出谁的推断比较科学合理,能直实地反映公司全体员工月收入水平。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2;
(3)△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴;
(4)△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)5x-1=x+1
(2)2x+3(2x-1)=16-(x+1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司购买了一批
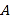 、
、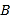 型芯片,其中
型芯片,其中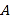 型芯片的单价比
型芯片的单价比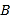 型芯片的单价少9元,已知该公司用3120元购买
型芯片的单价少9元,已知该公司用3120元购买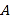 型芯片的条数与用4200元购买
型芯片的条数与用4200元购买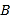 型芯片的条数相等.
型芯片的条数相等.(1)求该公司购买的
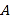 、
、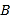 型芯片的单价各是多少元?
型芯片的单价各是多少元?(2)若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条
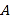 型芯片?
型芯片? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)题中的抛物线上有一个动点P,当点P在抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标;
(3)设(1)题中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数a在数轴上表示的点在原点左侧,距离原点3个单位长,b在数轴上表示的点在原点右侧,距离原点2个单位长,c和d互为倒数,m与n互为相反数,y为最大的负整数,求(y+b)2+m(a-cd)-nb2的值.
相关试题

