【题目】![]() 中,三个内角的平分线交于点
中,三个内角的平分线交于点![]() ,过点
,过点![]() 作
作![]() ,交边
,交边![]() 于点
于点![]() .
.
(1)如图,若∠ABC=40°,则∠AOC= ,∠ADO= ;
(2)猜想![]() 与
与![]() 的关系,并说明你的理由;
的关系,并说明你的理由;

参考答案:
【答案】(1) 110°, 110°(2)相等,证明见解析
【解析】
(1)根据内角和的性质得出∠BAC+∠BCA=180°-∠ABC=140°,
再利用角平分线的性质得到∠OAC+∠OCA=![]() (∠BAC+∠BCA)=70°,再根据三角形的内角和即可求出∠AOC;根据∠ADO是△BDO的一个外角即可求出其度数;
(∠BAC+∠BCA)=70°,再根据三角形的内角和即可求出∠AOC;根据∠ADO是△BDO的一个外角即可求出其度数;
(2)设∠ABC=a,根据①的方法求出∠AOC与∠ADO即可判断
(1)∵∠ABC=40°,∴∠BAC+∠BCA=180°-∠ABC=140°,
∵三个内角的平分线交于点![]() ,∴∠OAC+∠OCA=
,∴∠OAC+∠OCA=![]() (∠BAC+∠BCA)=70°,
(∠BAC+∠BCA)=70°,
∠AOC=180°-(∠OAC+∠OCA)=110°,
∵∠ADO是△BDO的一个外角,![]()
∴∠ADO=∠ABO+90°=![]() ∠ABC+90°=110°.
∠ABC+90°=110°.
(2)相等,证明如下:
设∠ABC=a,
根据①的方法求出∠AOC=180°-(∠OAC+∠OCA)
=180°-![]() (∠BAC+∠BCA)
(∠BAC+∠BCA)
= 180°-![]() (180°-a)
(180°-a)
=90°+![]() a
a
∠ADO =∠ABO+90°
=![]() ∠ABC+90°
∠ABC+90°
=![]() a+90°
a+90°
故![]() =
=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(﹣1,0)和(m,0),且1<m<2,当x<﹣1时,y随着x的增大而减小.下列结论:
①abc>0;
②a+b>0;
③若点A(﹣3,y1),点B(3,y2)都在抛物线上,则y1<y2;
④a(m﹣1)+b=0;
⑤若c≤﹣1,则b2﹣4ac≤4a.
其中结论错误的是 . (只填写序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+ax+a﹣2=0
(1)若该方程的一个根为1,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程总有两个不相等的实数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a、b的式子表示);
(2)应用:点A为线段BC外一动点,且BC=4,AB=2,如图2,分别以AB、AC为边,作等边三角形ABD和等边△ACE,连接CD、BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值;
③直接写出△DBC面积的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,水平放置的圆柱形排水管的截面为⊙O,有水部分弓形的高为2,弦AB=4
 ,求⊙O的半径.
,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ABC的顶点A在△ECD的斜边DE上.
(1)求证AE2+AD2=2AC2 ;
(2)如图2,过点C作CO垂直AB于0点并延长交DE于点F,请确定线段AE、AF、DF间的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地匀速驶向B地,甲车比乙车早出发2小时,并且甲车图中休息了0.5小时后仍以原速度驶向B地,如图是甲、乙两车行驶的路程y(千米)与行驶的时间x(小时)之间的函数图象.下列说法:
①m=1,a=40;
②甲车的速度是40千米/小时,乙车的速度是80千米/小时;
③当甲车距离A地260千米时,甲车所用的时间为7小时;
④当两车相距20千米时,则乙车行驶了3或4小时,
其中正确的个数是( )
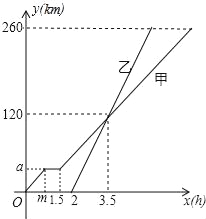
A. 1个B. 2个C. 3个D. 4个
相关试题

