【题目】如图,水平放置的圆柱形排水管的截面为⊙O,有水部分弓形的高为2,弦AB=4 ![]() ,求⊙O的半径.
,求⊙O的半径.
参考答案:
【答案】解:过点O作OC⊥AB于点C,交 ![]() 于点D,连接OB,
于点D,连接OB, 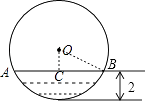
设⊙O的半径为r,则OC=r﹣2,
∵OC⊥AB,
∴BC= ![]() AB=
AB= ![]() ×4
×4 ![]() =2
=2 ![]() ,
,
在Rt△BOC中,
∵OC2+BC2=OB2,即(r﹣2)2+(2 ![]() )2=r2,
)2=r2,
解得r=4.
【解析】此类问题通过添加辅助线过点O作OC⊥AB于点C,交弧AB于点D,连接OB,根据垂径定理求出BC的长,再用含r的代数式表示出OC的长,然后根据勾股定理建立方程求解即可。
【考点精析】通过灵活运用勾股定理的概念和垂径定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+ax+a﹣2=0
(1)若该方程的一个根为1,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程总有两个不相等的实数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a、b的式子表示);
(2)应用:点A为线段BC外一动点,且BC=4,AB=2,如图2,分别以AB、AC为边,作等边三角形ABD和等边△ACE,连接CD、BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值;
③直接写出△DBC面积的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
 中,三个内角的平分线交于点
中,三个内角的平分线交于点 ,过点
,过点 作
作 ,交边
,交边 于点
于点 .
.(1)如图,若∠ABC=40°,则∠AOC= ,∠ADO= ;
(2)猜想
 与
与 的关系,并说明你的理由;
的关系,并说明你的理由;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ABC的顶点A在△ECD的斜边DE上.
(1)求证AE2+AD2=2AC2 ;
(2)如图2,过点C作CO垂直AB于0点并延长交DE于点F,请确定线段AE、AF、DF间的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地匀速驶向B地,甲车比乙车早出发2小时,并且甲车图中休息了0.5小时后仍以原速度驶向B地,如图是甲、乙两车行驶的路程y(千米)与行驶的时间x(小时)之间的函数图象.下列说法:
①m=1,a=40;
②甲车的速度是40千米/小时,乙车的速度是80千米/小时;
③当甲车距离A地260千米时,甲车所用的时间为7小时;
④当两车相距20千米时,则乙车行驶了3或4小时,
其中正确的个数是( )
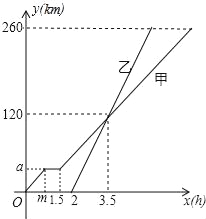
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于点E,若AB=4,BC=8,则△ACE的面积为_____.
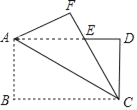
相关试题

