Question

【题目】(1)发现：如图1，点A为线段BC外一动点，且BC＝a，AB＝b．

填空：当点A位于　 　时，线段AC的长取得最大值，且最大值为　 　(用含a、b的式子表示)；

(2)应用：点A为线段BC外一动点，且BC＝4，AB＝2，如图2，分别以AB、AC为边，作等边三角形ABD和等边△ACE，连接CD、BE．

①请找出图中与BE相等的线段，并说明理由；

②直接写出线段BE长的最大值；

③直接写出△DBC面积的最大值．

Answer 1

【答案】(1)CB的延长线上，a+b；(2)①CD＝BE，理由见解析；②6；③4.

【解析】

（1）根据点A位于CB的延长线上时，线段AC的长取得最大值，即可得到结论；

（2）①根据等边三角形的性质得到AD＝AB，AC＝AE，∠BAD＝∠CAE＝60°，推出△CAD≌△EAB，根据全等三角形的性质得到CD＝BE；

②由于线段BE长的最大值＝线段CD的最大值，根据（1）中的结论即可得到结果；

③作DP⊥CB，交CB延长线于点P，当DB⊥BC时，DP取得最大值，最大值为2，再根据三角形的面积公式求解可得．

(1)∵点A为线段BC外一动点，且BC＝a，AB＝b，

∴当点A位于CB的延长线上时，线段AC的长取得最大值，且最大值为BC+AB＝a+b，

故答案为：CB的延长线上，a+b；

(2)①CD＝BE，

理由：∵△ABD与△ACE是等边三角形，

∴AD＝AB，AC＝AE，∠BAD＝∠CAE＝60°，

∴∠BAD+∠BAC＝∠CAE+∠BAC，

即∠CAD＝∠EAB，

在△CAD与△EAB中，

∵

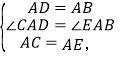
∴△CAD≌△EAB(SAS)，

∴CD＝BE；

②∵线段BE长的最大值＝线段CD的最大值，

由(1)知，当线段CD的长取得最大值时，点D在CB的延长线上，

∴最大值为BD+BC＝AB+BC＝6；

③如图，过点D作DP⊥CB，交CB延长线于点P，

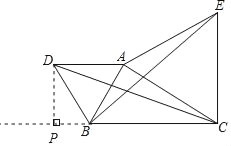
在Rt△BDP中，DP＜DB，

当DB⊥BC时，DP取得最大值，最大值为2，

∴△DBC面积的最大值为