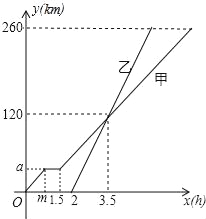
【题目】甲、乙两车从A地匀速驶向B地,甲车比乙车早出发2小时,并且甲车图中休息了0.5小时后仍以原速度驶向B地,如图是甲、乙两车行驶的路程y(千米)与行驶的时间x(小时)之间的函数图象.下列说法:
①m=1,a=40;
②甲车的速度是40千米/小时,乙车的速度是80千米/小时;
③当甲车距离A地260千米时,甲车所用的时间为7小时;
④当两车相距20千米时,则乙车行驶了3或4小时,
其中正确的个数是( )
A. 1个B. 2个C. 3个D. 4个
参考答案:
【答案】C
【解析】
①观察图象找出点(3.5,120),根据“速度=路程÷行驶时间”可以算出甲车的速度,再结合甲车中途休息半个小时即可得出a、m的值;
②根据点(3.5,120),利用“速度=路程÷行驶时间”可以算出乙车的速度;
③根据“时间=路程÷速度”可算出甲车距离A地260千米时行驶的时间,加上休息的0.5小时即可得出结论;
④根据点(3.5,120),结合两车速度差即可算出当两车相距20千米时,甲车行驶的时间,再根据甲车比乙车早出发2小时可得出乙车行驶时间.
对比给定的说法即可得出结论.
①∵甲车途中休息了0.5小时,
∴m=1.5﹣0.5=1,
甲车的速度为:120÷(3.5﹣0.5)=40(千米/小时).
a=1×40=40.
∴①成立;
②乙车的速度为:120÷(3.5﹣2)=80(千米/时),
∴甲车的速度是40千米/小时,乙车的速度是80千米/小时,②成立;
③当甲车距离A地260千米时,甲车所用的时间为:260÷40+0.5=7(小时),
∴③成立;
④∵两车相遇时时间为3.5时,且甲车速度为40千米/时,乙车速度为80千米/时,
∴当两车相距20千米时,甲车行驶的时间为:3.5+20÷(80﹣40)=4(小时)或3.5﹣20÷(80﹣40)=3(小时),
又∵甲车比乙车早出发2小时,
∴当两车相距20千米时,则乙车行驶了1或2小时,④不正确.
综上可知:正确的结论有①②③.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 中,三个内角的平分线交于点
中,三个内角的平分线交于点 ,过点
,过点 作
作 ,交边
,交边 于点
于点 .
.(1)如图,若∠ABC=40°,则∠AOC= ,∠ADO= ;
(2)猜想
 与
与 的关系,并说明你的理由;
的关系,并说明你的理由;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,水平放置的圆柱形排水管的截面为⊙O,有水部分弓形的高为2,弦AB=4
 ,求⊙O的半径.
,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ABC的顶点A在△ECD的斜边DE上.
(1)求证AE2+AD2=2AC2 ;
(2)如图2,过点C作CO垂直AB于0点并延长交DE于点F,请确定线段AE、AF、DF间的数量关系,并证明你的结论.

-
科目: 来源: 题型:
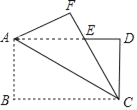
查看答案和解析>>【题目】如图,将长方形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于点E,若AB=4,BC=8,则△ACE的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
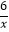 (x>0)的图象交于A(m,6),B(3,n)两点
(x>0)的图象交于A(m,6),B(3,n)两点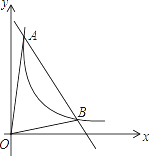
(1)求一次函数的解析式;
(2)根据图象直接写出使kx+b<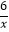 成立的x的取值范围;
成立的x的取值范围;
(3)求△AOB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过点A1(1,0)作x轴的垂线,交直线y=2x于点B1;点A2与点O关于直线A1B1对称;过点A2(2,0)作x轴的垂线,交直线y=2x于点B2;点A3与点O关于直线A2B2对称;过点A3(4,0)作x轴的垂线,交直线y=2x于点B3;…,按此规律作下去,则点Bn的坐标为_____.

相关试题

