Question

【题目】抛物线y=ax2+bx+c（a，b，c为常数，且a≠0）经过点（﹣1，0）和（m，0），且1＜m＜2，当x＜﹣1时，y随着x的增大而减小．下列结论：
①abc＞0；
②a+b＞0；
③若点A（﹣3，y1），点B（3，y2）都在抛物线上，则y1＜y2；
④a（m﹣1）+b=0；
⑤若c≤﹣1，则b2﹣4ac≤4a．
其中结论错误的是 ． （只填写序号）

Answer 1

【答案】③⑤
【解析】解：如图，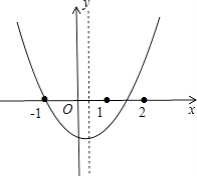

∵抛物线开口向上，

∴a＞0，

∵抛物线的对称轴在y轴的右侧，

∴b＜0，

∵抛物线与y轴的交点在x轴下方，

∴c＜0，

∴abc＞0，所以①的结论正确；

∵抛物线过点（﹣1，0）和（m，0），且1＜m＜2，

∴0＜﹣ ＜ ，

∴ + = ＞0，∴a+b＞0，所以②的结论正确；

∵点A（﹣3，y1）到对称轴的距离比点B（3，y2）到对称轴的距离远，

∴y1＞y2，所以③的结论错误；

∵抛物线过点（﹣1，0），（m，0），

∴a﹣b+c=0，am2+bm+c=0，

∴am2﹣a+bm+b=0，

a（m+1）（m﹣1）+b（m+1）=0，

∴a（m﹣1）+b=0，所以④的结论正确；

∵ ＜c，

而c≤﹣1，

∴ ＜﹣1，

∴b2﹣4ac＞4a，所以⑤的结论错误．

故答案为③⑤．

先根据题意画出抛物线的大致图像，观察函数图像的开口方向、对称轴的位置、抛物线与两坐标轴的位置可知：a＞0，b＜0，c＜0，可对①作出判断；根据抛物线过点（﹣1，0）和（m，0），且1＜m＜2，结合对称轴方程可得出a+b＞0，可对②作出判断；由点A（﹣3，y1），点B（3，y2）都在抛物线上，可根据两点到对称轴的距离远近对③作出判断；将（﹣1，0），（m，0），分别代入函数解析式，建立方程组，将两方程相减，再将方程变形即可对④作出判断；观察图像可知抛物线的顶点纵坐标＜c，且c≤﹣1，建立不等式通过变形可对⑤作出判断。