【题目】已知![]() 是
是![]() 的
的![]() 边上一点,连结
边上一点,连结![]() ,此时有结论
,此时有结论![]() ,请解答下列问题:
,请解答下列问题:
(1)当![]() 是
是![]() 边上的中点时,
边上的中点时,![]() 的面积
的面积 ![]() 的面积(填“>”“<”或“=”).
的面积(填“>”“<”或“=”).
(2)如图1,点![]() 分别为
分别为![]() 边上的点,连结
边上的点,连结![]() 交于点
交于点![]() ,若
,若![]() 、
、![]() 、
、![]() 的面积分别为5,8,10,则
的面积分别为5,8,10,则![]() 的面积是 (直接写出结论).
的面积是 (直接写出结论).
(3)如图2,若点![]() 分别是
分别是![]() 的
的![]() 边上的中点,且
边上的中点,且![]() ,求四边形
,求四边形![]() 的面积.可以用如下方法:连结
的面积.可以用如下方法:连结![]() ,由
,由![]() 得
得![]() ,同理:
,同理:![]() ,设
,设![]() ,
,![]() ,则
,则![]() ,
,![]() ,由题意得
,由题意得![]() ,
,![]() ,可列方程组为:
,可列方程组为:![]() ,解得
,解得![]() ,可得四边形
,可得四边形![]() 的面积为20.解答下面问题:
的面积为20.解答下面问题:
如图3,![]() 是
是![]() 的三等分点,
的三等分点,![]() 是
是![]() 的三等分点,
的三等分点,![]() 与
与![]() 交于
交于![]() ,且
,且![]() ,请计算四边形
,请计算四边形![]() 的面积,并说明理由.
的面积,并说明理由.



图1 图2 图3
参考答案:
【答案】(1)=;(2)18;(3)![]() ,见解析
,见解析
【解析】
(1)利用同高(或同底)的三角形面积比等于对应边(或高)的比即可得.
(2)联结![]() ,利用同高的三角形面积比等于对应边的比,结合已知条件联立方程可得.
,利用同高的三角形面积比等于对应边的比,结合已知条件联立方程可得.
(3)联结![]() ,利用同高的三角形面积比等于对应边的比,结合已知条件联立方程可得.
,利用同高的三角形面积比等于对应边的比,结合已知条件联立方程可得.
(1)∵![]() ,
,![]() 是
是![]() 边上的中点
边上的中点
∴![]() ,则
,则![]()
(2)如图,连结![]()

∵![]() 、
、![]() 、
、![]() 的面积分别为5,8,10,
的面积分别为5,8,10,
∴![]() ,
,![]()
∴![]()
设![]() ,
,![]()
则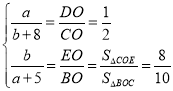
整理得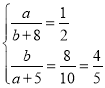 解得
解得![]() ,
,
则![]() .
.
(3)连结![]() ,设
,设![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
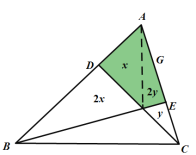
∵![]() ,
,![]()
∴![]()
∵![]() ,
,![]()
∴![]()
则可列方程组![]()
![]() ,加减消元法
,加减消元法
解得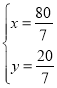
∴四边形![]() 的面积为:
的面积为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 经过点
经过点 ,
, .
.
(1)求直线
 的解析式;
的解析式;(2)若直线
 与直线
与直线 相交于点
相交于点 ,求点
,求点 的坐标;
的坐标;(3)根据图象,直接写出关于
 的不等式
的不等式 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+c与x轴交于A,B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,﹣3),B(4,0).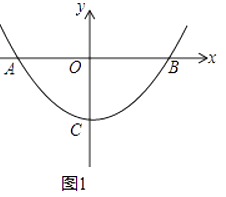
①求该抛物线的解析式;
②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2)如图2,已知直线PA,PB与y轴分别交于E、F两点.当点P运动时, 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )

A.
B.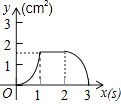
C.
D.
-
科目: 来源: 题型:
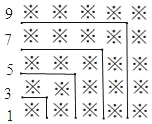
查看答案和解析>>【题目】探索规律,观察下面由※组成的图案和算式,并解答问题.
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)试写出1+3+5+7+9+…+19= ;
(2)试写出1+3+5+7+9+…+(2n﹣1)= ;
(3)请用上述规律计算:
①101+103+105+107+…+2017+2019;
②(2m+1)+(2m+3)+(2m+5)+…+(2n+7)(其中n>m)(列出代数式即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地城管需要从甲、乙两个仓库向A、B两地分别运送10吨和5吨的防寒物资,甲、乙两仓库分别有8吨、7吨防寒物资.从甲、乙两仓库运送防寒物资到A、B两地的运费单价(元/吨)如表1,设从甲仓库运送到A地的防寒物资为x吨(如表2).
表1
甲仓库
乙仓库
A地
80
100
B地
60
40
表2
甲仓库
乙仓库
A地
10-x
B地
(1)完成表2;
(2)求运送的总运费y(元)与x(吨)之间的函数表达式,并直接写出x的取值范围;
(3)求最低总运费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角板ABC中,∠ACB=90°,∠B=30°,AC=2
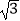 ,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )
,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( ) 
A. π
π
B.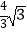 π
π
C.2π
D.3π
相关试题

