【题目】抛物线y=ax2+c与x轴交于A,B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,﹣3),B(4,0).
①求该抛物线的解析式;
②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2)如图2,已知直线PA,PB与y轴分别交于E、F两点.当点P运动时, ![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
参考答案:
【答案】
(1)解:①将P(1,﹣3),B(4,0)代入y=ax2+c,得
![]() ,解得
,解得  ,
,
抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() ;
;
②如图1,
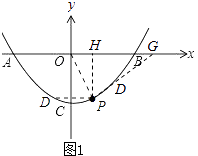
当点D在OP左侧时,
由∠DPO=∠POB,得
DP∥OB,
D与P关于y轴对称,P(1,﹣3),
得D(﹣1,﹣3);
当点D在OP右侧时,延长PD交x轴于点G.
作PH⊥OB于点H,则OH=1,PH=3.
∵∠DPO=∠POB,
∴PG=OG.
设OG=x,则PG=x,HG=x﹣1.
在Rt△PGH中,由x2=(x﹣1)2+32,得x=5.
∴点G(5,0).
∴直线PG的解析式为y= ![]() x﹣
x﹣ ![]()
解方程组 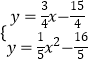 得
得 ![]() ,
,  .
.
∵P(1,﹣3),
∴D( ![]() ,﹣
,﹣ ![]() ).
).
∴点D的坐标为(﹣1,﹣3)或( ![]() ,﹣
,﹣ ![]() )
)
(2)解:点P运动时, ![]() 是定值,定值为2,理由如下:
是定值,定值为2,理由如下:
作PQ⊥AB于Q点,设P(m,am2+c),A(﹣t,0),B(t,0),则at2+c=0,c=﹣at2.
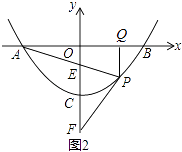
∵PQ∥OF,
∴ ![]() ,
,
∴OF= ![]() =﹣
=﹣ ![]() =
= ![]() =amt+at2.
=amt+at2.
同理OE=﹣amt+at2.
∴OE+OF=2at2=﹣2c=2OC.
∴ ![]() =2.
=2.
【解析】(1)①根据待定系数法求函数解析式,可得答案;②根据平行线的判定,可得PD∥OB,根据函数值相等两点关于对称轴对称,可得D点坐标;(2)根据待定系数法,可得E、F点的坐标,根据分式的性质,可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1所示,是由几个小立方块所搭几何体的俯视图,小立方块中的数字表示在该位置小立方块的个数.请画出从正面和从左面看到的这个几何体的形状图.(注意:画得不规范不给分)
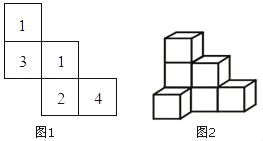
从正面看:
从左面看:
(2)如图2,一次数学活动课上,小明用7个棱长为1cm的小立方块积木搭成的几何体,然后他请小亮用尽可能少的同样大小的立方块在旁边再搭一个几何体,使小亮所搭的几何体恰好可以和小明所搭的几何体拼成一个大长方体(即拼大长方体时将其中一个几何体翻转,且假定组成每个几何体的立方块粘合在一起),则:
①小亮至少还需要 个小正方体;
②请画出小明所搭几何体的三视图,并计算①中小亮所搭几何体的表面积.
主视图:
俯视图:
左视图:
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励市民节约用水,万州市居民生活用水按阶梯式水价计费,表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:(水价计费
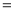 自来水销售费用
自来水销售费用 污水处理费用)
污水处理费用)自来水销售价格
污水处理价格
每户每月用水量
单价:元
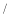 吨
吨单价:元
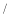 吨
吨17吨及以下
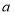
0.80
超过17吨不超过30吨的部分

0.80
超过30吨的部分
6.00
0.80
说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费;
已知小明家2013年3月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求
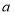 ,
, 的值.
的值.(2)随着夏天的到来,用水量将增加。为了节省开支,小梦计划把6月份的水费控制在不超过家庭月收入的2%,若小梦加的月收入为9200元,则小王家6月份最多能用水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 经过点
经过点 ,
, .
.
(1)求直线
 的解析式;
的解析式;(2)若直线
 与直线
与直线 相交于点
相交于点 ,求点
,求点 的坐标;
的坐标;(3)根据图象,直接写出关于
 的不等式
的不等式 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )

A.
B.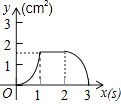
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是
是 的
的 边上一点,连结
边上一点,连结 ,此时有结论
,此时有结论 ,请解答下列问题:
,请解答下列问题:(1)当
 是
是 边上的中点时,
边上的中点时, 的面积
的面积  的面积(填“>”“<”或“=”).
的面积(填“>”“<”或“=”).(2)如图1,点
 分别为
分别为 边上的点,连结
边上的点,连结 交于点
交于点 ,若
,若 、
、 、
、 的面积分别为5,8,10,则
的面积分别为5,8,10,则 的面积是 (直接写出结论).
的面积是 (直接写出结论).(3)如图2,若点
 分别是
分别是 的
的 边上的中点,且
边上的中点,且 ,求四边形
,求四边形 的面积.可以用如下方法:连结
的面积.可以用如下方法:连结 ,由
,由 得
得 ,同理:
,同理: ,设
,设 ,
, ,则
,则 ,
, ,由题意得
,由题意得 ,
, ,可列方程组为:
,可列方程组为: ,解得
,解得 ,可得四边形
,可得四边形 的面积为20.解答下面问题:
的面积为20.解答下面问题:如图3,
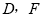 是
是 的三等分点,
的三等分点, 是
是 的三等分点,
的三等分点, 与
与 交于
交于 ,且
,且 ,请计算四边形
,请计算四边形 的面积,并说明理由.
的面积,并说明理由.


图1 图2 图3
-
科目: 来源: 题型:
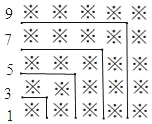
查看答案和解析>>【题目】探索规律,观察下面由※组成的图案和算式,并解答问题.
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)试写出1+3+5+7+9+…+19= ;
(2)试写出1+3+5+7+9+…+(2n﹣1)= ;
(3)请用上述规律计算:
①101+103+105+107+…+2017+2019;
②(2m+1)+(2m+3)+(2m+5)+…+(2n+7)(其中n>m)(列出代数式即可)
相关试题

