【题目】三角板ABC中,∠ACB=90°,∠B=30°,AC=2 ![]() ,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )
,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( ) 
A.![]() π
π
B.![]() π
π
C.2π
D.3π
参考答案:
【答案】C
【解析】解:∵∠B=30°,AC=2 ![]() ,
,
∴BA=4 ![]() ,∠A=60°,
,∠A=60°,
∴CB=6,
∵AC=A′C,
∴∠AA′C是等边三角形,
∴∠ACA′=60°,
∴∠BCB′=60°,
∴弧长l= ![]() =
= ![]() =2π,
=2π,
故选C.
【考点精析】解答此题的关键在于理解弧长计算公式的相关知识,掌握若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是
是 的
的 边上一点,连结
边上一点,连结 ,此时有结论
,此时有结论 ,请解答下列问题:
,请解答下列问题:(1)当
 是
是 边上的中点时,
边上的中点时, 的面积
的面积  的面积(填“>”“<”或“=”).
的面积(填“>”“<”或“=”).(2)如图1,点
 分别为
分别为 边上的点,连结
边上的点,连结 交于点
交于点 ,若
,若 、
、 、
、 的面积分别为5,8,10,则
的面积分别为5,8,10,则 的面积是 (直接写出结论).
的面积是 (直接写出结论).(3)如图2,若点
 分别是
分别是 的
的 边上的中点,且
边上的中点,且 ,求四边形
,求四边形 的面积.可以用如下方法:连结
的面积.可以用如下方法:连结 ,由
,由 得
得 ,同理:
,同理: ,设
,设 ,
, ,则
,则 ,
, ,由题意得
,由题意得 ,
, ,可列方程组为:
,可列方程组为: ,解得
,解得 ,可得四边形
,可得四边形 的面积为20.解答下面问题:
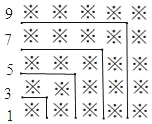
的面积为20.解答下面问题:如图3,
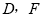 是
是 的三等分点,
的三等分点, 是
是 的三等分点,
的三等分点, 与
与 交于
交于 ,且
,且 ,请计算四边形
,请计算四边形 的面积,并说明理由.
的面积,并说明理由.


图1 图2 图3
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律,观察下面由※组成的图案和算式,并解答问题.
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)试写出1+3+5+7+9+…+19= ;
(2)试写出1+3+5+7+9+…+(2n﹣1)= ;
(3)请用上述规律计算:
①101+103+105+107+…+2017+2019;
②(2m+1)+(2m+3)+(2m+5)+…+(2n+7)(其中n>m)(列出代数式即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地城管需要从甲、乙两个仓库向A、B两地分别运送10吨和5吨的防寒物资,甲、乙两仓库分别有8吨、7吨防寒物资.从甲、乙两仓库运送防寒物资到A、B两地的运费单价(元/吨)如表1,设从甲仓库运送到A地的防寒物资为x吨(如表2).
表1
甲仓库
乙仓库
A地
80
100
B地
60
40
表2
甲仓库
乙仓库
A地
10-x
B地
(1)完成表2;
(2)求运送的总运费y(元)与x(吨)之间的函数表达式,并直接写出x的取值范围;
(3)求最低总运费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,以AD为底边作等腰△ADE,将△ADE沿DE折叠,点A落到点F处,连接EF刚好经过点C,再连接AF,分别交DE于G,交CD于H.在下列结论中:
①△ABM≌△DCN;②∠DAF=30°;③△AEF是等腰直角三角形;④EC=CF;⑤S△HCF=S△ADH ,
其中正确的结论有( )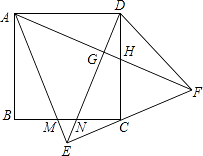
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,若AB=4,BC=6,则FD的长为 .
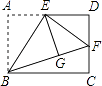
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是 .

相关试题

