【题目】某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50m.设饲养室长为x(m),占地面积为y(m2).
(1)如图1,问饲养室长x为多少时,占地面积y最大?
(2)如图2,现要求在图中所示位置留2m宽的门,且仍使饲养室的占地面积最大,小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.
参考答案:
【答案】
(1)解:∵y=x ![]() =﹣
=﹣ ![]() (x﹣25)2+
(x﹣25)2+ ![]() ,
,
∴当x=25时,占地面积最大,
即饲养室长x为25m时,占地面积y最大
(2)解:∵y=x ![]() =﹣
=﹣ ![]() (x﹣26)2+338,
(x﹣26)2+338,
∴当x=26时,占地面积最大,
即饲养室长x为26m时,占地面积y最大;
∵26﹣25=1≠2,
∴小敏的说法不正确
【解析】(1)根据题意用含x的代数式表示出饲养室的宽,由矩形的面积y=长×宽,列出y与x的函数关系式,再将函数解析式转化为顶点式,即可得出答案。
(2)根据题意用含x的代数式表示出饲养室的宽,根据矩形的面积=长×宽,列出y与x的函数关系式,再根据二次函数的性质分析即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点 E 在正方形 ABCD 的 AB 边上(不与点 A,B 重合),BD 是对角线,延长 AB 到点 F,使 BF=AE,过点 E 作 BD 的垂线,垂足为 M,连接 AM,CF.
(1)求证:MB=ME;
(2)①用等式表示线段 AM 与 CF 的数量关系,并证明;
②用等式表示线段 AM,BM,DM 之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某菜农搭建了一个横截面为抛物线的大棚,尺寸如图,若菜农身高为1.8m,他在不弯腰的情况下,在棚内的横向活动范围是m.
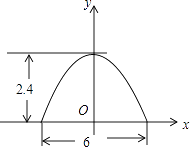
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了改善小区环境,某小区决定要在一块一边靠墙(墙长 25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为 40m 的栅栏围住(如图).设绿化带的BC 边长为x m,绿化带的面积为y m2 .
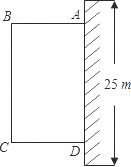
(1)求y 与x 之间的函数关系式,并写出自变量x 的取值范围.
(2)当x 为何值时,满足条件的绿化带的面积最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图, CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,∠CEF=60°,则∠ACB=______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是( ).

A.1
B.2
C.
D.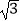
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:A(0,3),B(3,0),C(3,4)三点,点P(x,﹣0.5x),当△ABP的面积等于△ABC的面积时,则P点的坐标是_____.
相关试题

