【题目】列方程解应用题:
甲组的5名工人9月份完成的总工作量比此月人均定额的4倍多30件,乙组的6名工人9月份完成的总工作量比此月人均定额的6倍少30件
(1)如果两组工人实际完成的此月人均工作量相等,那么此月人均定额是多少?
(2)如果甲组工人实际完成的此月人均工作量比乙组的多3件,则此月人均定额是多少?
(3)如果甲组工人实际完成的此月人均工作量比乙组的少3件,则此月人均定额是多少?
参考答案:
【答案】(1)此月人均定额是55件;(2):此月人均定额是40件;(3)此月人均定额是70件.
【解析】
设此月人均定额为x件,则甲组的总工作量为(4x+30)件,人均为![]() 件;乙组的总工作量为(6x-30)件,乙组人均为(x-5)件.
件;乙组的总工作量为(6x-30)件,乙组人均为(x-5)件.
(1)根据两组人均工作量相等,即可得出关于x的一元一次方程,解之即可得出结论;
(2)根据甲组的人均工作量比乙组多3件,即可得出关于x的一元一次方程,解之即可得出结论;
(3)根据甲组的人均工作量比乙组少3件,即可得出关于x的一元一次方程,解之即可得出结论.
解:设此月人均定额为x件,则甲组的总工作量为(4x+30)件,人均为![]() 件;乙组的总工作量为(6x﹣30)件,乙组人均为(x﹣5)件.
件;乙组的总工作量为(6x﹣30)件,乙组人均为(x﹣5)件.
(1)∵两组人均工作量相等,
∴![]() =x﹣5,
=x﹣5,
解得:x=55.
答:此月人均定额是55件.
(2)∵甲组的人均工作量比乙组多3件,
∴![]() ﹣3=x﹣5,
﹣3=x﹣5,
解得:x=40.
答:此月人均定额是40件.
(3)∵甲组的人均工作量比乙组少3件,
∴![]() +3=x﹣5,
+3=x﹣5,
解得:x=70,
答:此月人均定额是70件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax+bx+c的图像如图所示,则代数式(a+b)-c的值( ).
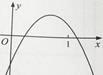
A.大于0
B.等于0
C.小于0
D.不确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.

(1)求证:AP⊥BQ;
(2)若AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在
 处,
处,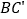 交AD于点E.
交AD于点E.(1)试判断△BDE的形状,并说明理由;
(2)若
 ,
, ,求△BDE的面积.
,求△BDE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
(1)若0<x≤6,请写出y与x的函数关系式.
(2)若x>6,请写出y与x的函数关系式.
(3)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解决问题:
一辆货车从超市出发,向东走了3千米到达小彬家,继续走2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小彬家,小颖家的位置.
(2)小明家距小彬家多远?
(3)货车一共行驶了多少千米?
(4)货车每千米耗油0.2升,这次共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形 ABCD 中,AB=AD,AC=5,∠DAB=∠DCB=90°, 则四边形 ABCD 的面积为( )
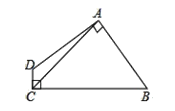
A. 15 B. 14.5 C. 13 D. 12.5
相关试题

