【题目】如图,在![]() 中,
中,![]() ,
,![]() 厘米,
厘米,![]() 厘米,
厘米,![]() 、
、![]() 是
是![]() 边上的两个动点,其中点
边上的两个动点,其中点![]() 从点
从点![]() 开始沿
开始沿![]() 方向运动,速度为1厘米/秒,点
方向运动,速度为1厘米/秒,点![]() 从点
从点![]() 开始沿
开始沿![]() 方向运动,速度为2厘米/秒,若它们同时出发,设出发的时间为
方向运动,速度为2厘米/秒,若它们同时出发,设出发的时间为![]() 秒.
秒.

(1)求出发2秒后,![]() 的长.
的长.
(2)点![]() 在
在![]() 边上运动时,当
边上运动时,当![]() 成为等腰三角形时,求点
成为等腰三角形时,求点![]() 的运动时间.
的运动时间.
参考答案:
【答案】(1)![]() cm (2)当t为5.5秒或6秒或6.6秒时,△BCQ为等腰三角形.
cm (2)当t为5.5秒或6秒或6.6秒时,△BCQ为等腰三角形.
【解析】
(1)根据点P、Q的运动速度求出AP,再求出BP和BQ,用勾股定理求得PQ即可;
(2)当点Q在边CA上运动时,能使△BCQ成为等腰三角形的运动时间有三种情况:
①当CQ=BQ时(图1),则∠C=∠CBQ,可证明∠A=∠ABQ,则BQ=AQ,则CQ=AQ,从而求得t;
②当CQ=BC时(图2),则BC+CQ=12,易求得t;
③当BC=BQ时(图3),过B点作BE⊥AC于点E,则求出BE,CE,即可得出t.
解:(1)BQ=2×2=4cm,
BP=AB-AP=8-2×1=6cm,
∵∠B=90°,
PQ= ![]() (cm);
(cm);
(2)解:分三种情况:
①当CQ=BQ时,如图1所示:
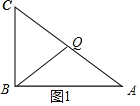
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°,
∠A+∠C=90°,
∴∠A=∠ABQ
∴BQ=AQ,
∴CQ=AQ=5,
∴BC+CQ=11,![]()
∴t=11÷2=5.5秒.
②当CQ=BC时,如图2所示:
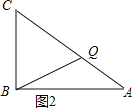
则BC+CQ=12
∴t=12÷2=6秒.
③当BC=BQ时,如图3所示:
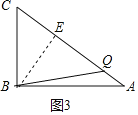
过B点作BE⊥AC于点E,
则BE= ![]() =4.8(cm)
=4.8(cm)
∴CE= ![]() =3.6cm,
=3.6cm,
∴CQ=2CE=7.2cm,
∴BC+CQ=13.2cm,
∴t=13.2÷2=6.6秒.
由上可知,当t为5.5秒或6秒或6.6秒时,△BCQ为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”n的各个数位上的数字之和记为F(n).例如n=135时,F(135)=1+3+5=9.
(1)对于“相异数”n,若F(n)=6,请你写出一个n的值;
(2)若a,b都是“相异数”,其中a=100x+12,b=350+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k=
 ,当F(a)+F(b)=18时,求k的最小值.
,当F(a)+F(b)=18时,求k的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是边长为1的等边三角形,
是边长为1的等边三角形, 是等腰直角三角形,且
是等腰直角三角形,且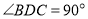 .
.
(1)求
 的长.
的长.(2)连接
 交
交 于点
于点 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(7分)某中学九年级学生在学习“直角三角形的边角关系”时,组织开展测量物体高度的实践活动.要测量学校一幢教学楼AB的高度如图所示,他们先在点C测得教学楼的顶部A的仰角为36.2°,然后向教学楼前进10米到达点D,又测得点A的仰角为45°.请你根据这些数据,求出这幢教学楼AB的高度.(结果精确到1米)
【参考数据:sin36.2°=0.59,cos36.2°=0.81,tan36.2°=0.73】

-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A.
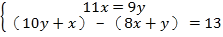
B.
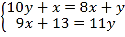
C.
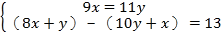
D.
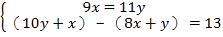
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,-2).
(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1 ,使它与△OAB的相似比为2:1,并分别写出点A、B的对应点A1、B1的坐标.
(2)画出将△OAB向左平移2个单位,再向上平移1个单位后的△O2A2B2 ,并写出点A、B的对应点A2、B2的坐标.
(3)判断△OA1B1与△O2A2B2 ,能否是关于某一点M为位似中心的位似图形,若是,请在图中标出位似中心M,并写出点M的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=12cm,BC=24cm,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积( )cm2.

A.72 B.90 C.108 D.144
相关试题

