【题目】如图,矩形ABCD中,AB=12cm,BC=24cm,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积( )cm2.

A.72 B.90 C.108 D.144
参考答案:
【答案】B.
【解析】
试题解析:由折叠得到△BCD≌△BC′D,由矩形ABCD得到△ABD≌△CDB,
∴△ABD≌△C′DB,
∴∠C′BD=∠ADB,
∴EB=DE,
在△ABE和△C′DE中,
 ,
,
∴△ABE≌△C′DE(AAS),
∴AE=C′E,
设AE=C′E=xcm,则有ED=AD-AE=(24-x)cm,
在Rt△ABE中,根据勾股定理得:AB2+AE2=BE2,即122+x2=(24-x)2,
解得:x=9,
∴AE=9cm,ED=15cm,
则S△BED=![]() EDAB=
EDAB=![]() ×15×12=90(cm2).
×15×12=90(cm2).
故选B
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,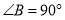 ,
, 厘米,
厘米, 厘米,
厘米, 、
、 是
是 边上的两个动点,其中点
边上的两个动点,其中点 从点
从点 开始沿
开始沿 方向运动,速度为1厘米/秒,点
方向运动,速度为1厘米/秒,点 从点
从点 开始沿
开始沿 方向运动,速度为2厘米/秒,若它们同时出发,设出发的时间为
方向运动,速度为2厘米/秒,若它们同时出发,设出发的时间为 秒.
秒.
(1)求出发2秒后,
 的长.
的长.(2)点
 在
在 边上运动时,当
边上运动时,当 成为等腰三角形时,求点
成为等腰三角形时,求点 的运动时间.
的运动时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A.
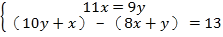
B.
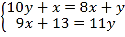
C.
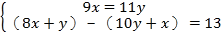
D.
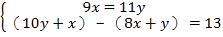
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,-2).
(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1 ,使它与△OAB的相似比为2:1,并分别写出点A、B的对应点A1、B1的坐标.
(2)画出将△OAB向左平移2个单位,再向上平移1个单位后的△O2A2B2 ,并写出点A、B的对应点A2、B2的坐标.
(3)判断△OA1B1与△O2A2B2 ,能否是关于某一点M为位似中心的位似图形,若是,请在图中标出位似中心M,并写出点M的坐标.

-
科目: 来源: 题型:
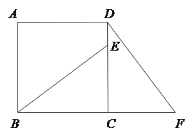
查看答案和解析>>【题目】已知:如图,在正方形ABCD中,E是CD边上的一点,F为BC延长线上一点,且CE=CF.
(1)求证:△BEC≌△DFC;
(2)如果BC+DF=9,CF=3,求正方形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题:
(1)本次调查属于 调查,样本容量是 ;
(2)请补全频数分布直方图中空缺的部分;
(3)求这50名学生每周课外体育活动时间的平均数;
(4)估计全校学生每周课外体育活动时间不少于6小时的人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点三角形A′B′C′是由格点三角形ABC通过怎样的平移得到的?
(2)如果以直线a,b为坐标轴建立平面直角坐标系后,点A的坐标为(-3,4),请写出格点三角形DEF各顶点的坐标,并求出三角形DEF的面积.

相关试题

