【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如图![]() 可以得到
可以得到![]()
![]() .请解答下列问题:
.请解答下列问题:

(1)写出图![]() 中所表示的数学等式;
中所表示的数学等式;

(2)利用(1)中所得到的结论,解决下面的问题:已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)小明同学打算用![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张相邻两边长为分别为
张相邻两边长为分别为![]() 、
、![]() 的长方形纸片拼出了一个面积为
的长方形纸片拼出了一个面积为 ![]() 长方形,那么他总共需要多少张纸片?
长方形,那么他总共需要多少张纸片?
参考答案:
【答案】(1)![]()
![]() ;(2)50;(3)143.
;(2)50;(3)143.
【解析】
(1)直接求得正方形的面积,再根据正方形的面积=各矩形的面积之和求解即可.
(2)将![]() ,
,![]() 代入(1)中得到的式子,然后计算即可;
代入(1)中得到的式子,然后计算即可;
(3)长方形的面积![]()
![]() ,然后运算多项式乘多项式,从而求得x、y、z的值,代入即可求解.
,然后运算多项式乘多项式,从而求得x、y、z的值,代入即可求解.
解:(1)![]()
![]()
(2)由(1)可知:![]()
![]()
![]()
(3)根据题意得,![]()
![]()
![]()
![]()
所以![]() ,
,![]() ,
,![]()
所以![]()
答:小明总共需要![]() 张纸。
张纸。
-
科目: 来源: 题型:
查看答案和解析>>【题目】要从甲、乙两名同学中选出一名,代表班级参加射击比赛. 现将甲、乙两名同学参加射击训练的成绩绘制成下列两个统计图:
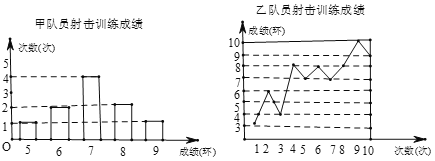
根据以上信息,整理分析数据如下:
平均成绩(环)
中位数(环)
众数(环)
方差(
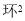 )
)甲
7
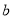
7
1. 2
乙
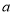
7. 5
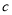
4. 2
(1)分别求表格中
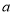 、
、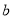 、
、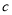 的值.
的值.(2)如果其他参赛选手的射击成绩都在7环左右,应该选______队员参赛更适合;如果其他参赛选手的射击成绩都在8环左右,应该选______队员参赛更适合.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“马航事件”的发生引起了我国政府的高度重视,我国政府迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止),此时的俯角为30°.为了便于观察,飞机继续向前飞行了800m到达B点,此时测得点F的俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A,B,C在同一直线上),竖直高度CF约为多少米?(结果保留整数.参考数据:
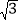 ≈1.7)
≈1.7)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是按规律排列的一组图形的前三个,观察图形,并在空白处填空

(1)第五个图形中,一共有_______个点
(2)请用n的代数式表示出第n个图形中点的数量__________
(3)第100个图形中一共有_______个点
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形
 的顶点
的顶点 与原点
与原点 重合,点
重合,点 在
在 轴的正半轴上,点
轴的正半轴上,点 在函数
在函数 的图象上,点
的图象上,点 的坐标为
的坐标为 .
.
(1)求
 的值.
的值.(2)将点
 沿
沿 轴正方向平移得到点
轴正方向平移得到点 ,当点
,当点 在函数
在函数 的图象上时,求
的图象上时,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式x2﹣4>0
解:∵x2﹣4=(x+2)(x﹣2)
∴x2﹣4>0可化为
(x+2)(x﹣2)>0
由有理数的乘法法则“两数相乘,同号得正”,得
①
 ②
②
解不等式组①,得x>2,
解不等式组②,得x<﹣2,
∴(x+2)(x﹣2)>0的解集为x>2或x<﹣2,
即一元二次不等式x2﹣4>0的解集为x>2或x<﹣2.
解答下列问题:
(1)一元二次不等式x2﹣25>0的解集为 ;
(2)分式不等式
 的解集为 ;
的解集为 ;(3)解一元二次不等式2x2﹣3x<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+3与x轴相交于点B,与y轴相交于点A,点E为线段AB中点,∠ABO的平分线BD与y轴相较于点D,点A、C关于点O对称.
x+3与x轴相交于点B,与y轴相交于点A,点E为线段AB中点,∠ABO的平分线BD与y轴相较于点D,点A、C关于点O对称.(1)求线段DE的长;
(2)一个动点P从点D出发,沿适当的路径运动到直线BC上的点F,再沿射线CB方向移动2
 个单位到点G,最后从点G沿适当的路径运动到点E处,当P的运动路径最短时,求此时点G的坐标;
个单位到点G,最后从点G沿适当的路径运动到点E处,当P的运动路径最短时,求此时点G的坐标;(3)将△ADE绕点A顺时针方向旋转,旋转角度α(0<α≤180°),在旋转过程中DE所在的直线分别与直线BC、直线AC相交于点M、点N,是否存在某一时刻使△CMN为等腰三角形,若存在,请求出CM的长,若不存在,请说明理由.

相关试题

