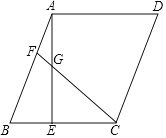
【题目】在ABCD中,AE⊥BC于点E,F为AB边上一点,连接CF,交AE于点G,CF=CB=AE.
(1)若AB![]() ,BC
,BC![]() ,求CE的长;
,求CE的长;
(2)求证:BE=CG﹣AG.
参考答案:
【答案】(1)![]() 1;(2)见解析.
1;(2)见解析.
【解析】
(1)在Rt△ABE中,由勾股定理求得BE,再由线段和差求得结果;
(2)延长GA到H,使得AH=BE,证明△ADH≌△EAB得DH=AB=CD,得∠DCH=∠DHC,再证明∠GHC=∠GCH得GC=GH便可得结果.
(1)∵CF=CB=AE,BC![]() ,
,
∴AE![]() ,
,
∵AE⊥BC于点E,AB![]() ,
,
∴BE![]() ,
,
∴CE=BC﹣BE![]() 1;
1;
(2)延长GA到H,使得AH=BE,连接DH,CH,
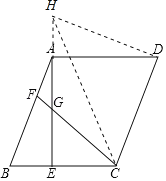
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵AE⊥BC,
∴∠AEB=∠DAE=90°,
∵BC=AE,
∴AE=DA,
在△ADH和△EAB中,
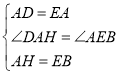 ,
,
∴△ADH≌△EAB(SAS),
∴DH=DC,∠DHA=∠ABE,
∴∠DHC=∠DCH,
∵CB=CF,
∴∠CBF=∠CFB,
∵AB∥CD,
∴∠CFB=∠DCF,
∴∠CBF=∠DCF,
∵∠DHA=∠ABE,
∴∠DHA=∠DCF,
∵∠DHC=∠DCH,
∴∠CHG=∠HCG,
∴CG=HG,即CG=AG+AH,
∴AH=CG﹣AG,
∵AH=BE,
∴BE=CG﹣AG,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,AC为直径,
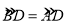 ,DE⊥BC,垂足为E.
,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)若CE=1,AC=4,求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是 ;表示﹣3和2两点之间的距离是 ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.如果表示数a和﹣2的两点之间的距离是3,那么a= ;
(2)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a取何值时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值是多少?请说明理由.
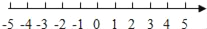
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
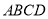 中,
中,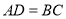 ,
,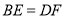 ,
, ,
,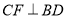 ,垂足分别为
,垂足分别为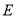 、
、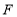 .
.
(1)求证:
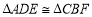 ;
;(2)若
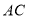 与
与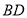 相交于点
相交于点 ,求证:
,求证: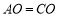 .
. -
科目: 来源: 题型:
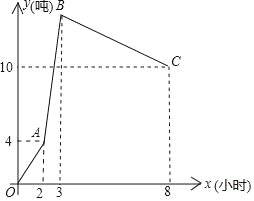
查看答案和解析>>【题目】某仓库有甲、乙、丙三辆运货车,每辆车只负责进货或出货,丙车每小时的运输量最多,乙车每小时的运输量最少,乙车每小时运6吨,如图是甲、乙、丙三辆运输车开始工作后,仓库的库存量y(吨)与工作时间x(小时)之间函数图象,其中OA段只有甲、丙两车参与运输,AB段只有乙、丙两车参与运输,BC段只有甲、乙两车参与运输.
(1)在甲、乙、丙三辆车中,出货车是 .(直接写出答案)
(2)甲车和丙车每小时各运输多少吨?
(3)由于仓库接到临时通知,要求三车在8小时后同时开始工作,但丙车在运送10吨货物后出现故障而退出,问:8小时后,甲、乙两车又工作了几小时,使仓库的库存量为8吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
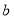 是最小的正整数,且
是最小的正整数,且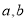 满足
满足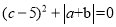 ,请回答:
,请回答:(1)请直接写出
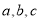 的值:
的值: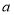 =______,
=______,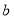 =______,
=______,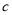 =______;
=______;(2)在(1)的条件下,若点P为一动点,其对应的数为
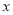 ,点P在0到2之间运动,即
,点P在0到2之间运动,即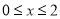 时,化简:
时,化简: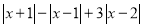 ;
;(3)在(1)(2)的条件下,
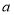 ,b,c分别对应的点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设
,b,c分别对应的点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设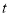 秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间
秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间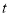 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=a(x+3)(x﹣1)(a≠0),与x轴从左至右依次相交于A、B两点,与y轴相交于点C,经过点A的直线y=﹣
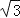 x+b与抛物线的另一个交点为D.
x+b与抛物线的另一个交点为D.(1)若点D的横坐标为2,求抛物线的函数解析式;
(2)若在第三象限内的抛物线上有点P,使得以A、B、P为顶点的三角形与△ABC相似,求点P的坐标;
(3)在(1)的条件下,设点E是线段AD上的一点(不含端点),连接BE.一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒
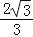 个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?
个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?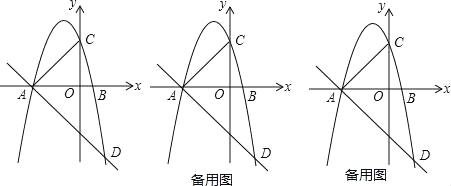
相关试题

