【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是 ;表示﹣3和2两点之间的距离是 ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.如果表示数a和﹣2的两点之间的距离是3,那么a= ;
(2)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a取何值时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值是多少?请说明理由.
![]()
参考答案:
【答案】(1)3;5;1或5;(2)6(3)9
【解析】
试题(1)根据数轴,观察两点之间的距离即可解决;
(2)根据|a+4|+|a-2|表示数a的点到-4与2两点的距离的和即可求解.
试题解析:(1)3;5;1或5;
(2)∵![]() 表示数轴上数
表示数轴上数![]() 和数-4,2之间距离的和,又因为
和数-4,2之间距离的和,又因为![]() 位于-4,2之间,
位于-4,2之间,
∴![]() 等于-4,2之间的距离和,
等于-4,2之间的距离和,
即![]() =|2-(-4)|=6.
=|2-(-4)|=6.
(3)∵![]() 表示数轴上数
表示数轴上数![]() 和数-5,1,4之间距离的和,
和数-5,1,4之间距离的和,
∴a=1时距离的和最小
∴![]() =
=![]() =|4-(-5)|=9
=|4-(-5)|=9
-
科目: 来源: 题型:
查看答案和解析>>【题目】校车安全是近几年社会关注的热门话题,其中超载和超速行驶是校车事故的主要原因.小亮和同学尝试用自己所学的三角函数知识检测校车是否超速,如下图,观测点设在到白田路的距离为100米的点P处.这时,一辆校车由西向东匀速行驶,测得此校车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO =45°.
(1)求A、B之间的路程;(参考数据:
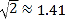 ,
, 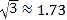 )
)(2)请判断此校车是否超过了白田路每小时60千米的限制速度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店一种商品的定价为每件50元.商店为了促销,决定如果购买5件以上,则超过5件的部分打七折.
(1)用表达式表示购买这种商品的货款
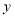 (元)与购买数量
(元)与购买数量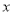 (件)之间的函数关系;
(件)之间的函数关系;(2)当
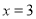 ,
,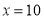 时,货款分别为多少元?
时,货款分别为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,AC为直径,
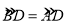 ,DE⊥BC,垂足为E.
,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)若CE=1,AC=4,求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
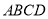 中,
中,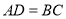 ,
,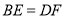 ,
, ,
,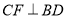 ,垂足分别为
,垂足分别为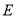 、
、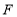 .
.
(1)求证:
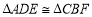 ;
;(2)若
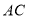 与
与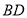 相交于点
相交于点 ,求证:
,求证: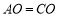 .
. -
科目: 来源: 题型:
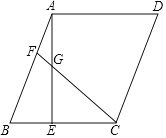
查看答案和解析>>【题目】在ABCD中,AE⊥BC于点E,F为AB边上一点,连接CF,交AE于点G,CF=CB=AE.
(1)若AB
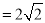 ,BC
,BC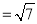 ,求CE的长;
,求CE的长;(2)求证:BE=CG﹣AG.
-
科目: 来源: 题型:
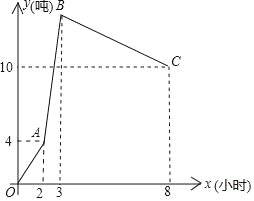
查看答案和解析>>【题目】某仓库有甲、乙、丙三辆运货车,每辆车只负责进货或出货,丙车每小时的运输量最多,乙车每小时的运输量最少,乙车每小时运6吨,如图是甲、乙、丙三辆运输车开始工作后,仓库的库存量y(吨)与工作时间x(小时)之间函数图象,其中OA段只有甲、丙两车参与运输,AB段只有乙、丙两车参与运输,BC段只有甲、乙两车参与运输.
(1)在甲、乙、丙三辆车中,出货车是 .(直接写出答案)
(2)甲车和丙车每小时各运输多少吨?
(3)由于仓库接到临时通知,要求三车在8小时后同时开始工作,但丙车在运送10吨货物后出现故障而退出,问:8小时后,甲、乙两车又工作了几小时,使仓库的库存量为8吨?
相关试题

