【题目】已知![]() 是最小的正整数,且
是最小的正整数,且![]() 满足
满足![]() ,请回答:
,请回答:
(1)请直接写出![]() 的值:
的值:![]() =______,
=______,![]() =______,
=______,![]() =______;
=______;
(2)在(1)的条件下,若点P为一动点,其对应的数为![]() ,点P在0到2之间运动,即
,点P在0到2之间运动,即![]() 时,化简:
时,化简:![]() ;
;
(3)在(1)(2)的条件下,![]() ,b,c分别对应的点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设
,b,c分别对应的点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设![]() 秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间
秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
![]()
参考答案:
【答案】(1)﹣1,1,5;(2)﹣x+6或﹣3x+8;(3)不变,BC﹣AB=2.
【解析】
(1)根据b是最小的正整数,即可确定b的值,然后根据非负数的性质,几个非负数的和是0,则每个数是0,即可求得a,b,c的值;
(2)分两种情况,根据x的取值范围,确定x+1,x-1,x-2的符号,然后根据绝对值的意义化简即可;
(3)先把AB,BC用含t的式示出来,再得到BC-AB=2,从而得出BC-AB的值为定值.
解:(1)依题意得,b=1,c﹣5=0,a+b=0
解得a=﹣1, b=1, c=5;
故答案为:﹣1,1,5;
(2)当点P在0到2之间运动时,0≤x≤2,
因此,分两种情况讨论:
①当0≤x≤1时,x+1>0,x﹣1≤0,x﹣2≤0,
原式=x+1﹣1+x+6﹣3x=﹣x+6;
②当1<x≤2时,x+1>0,x﹣1>0,x﹣2≤0,
原式=x+1﹣x+1+6﹣3x=﹣3x+8;
综上,化简![]() 的结果为﹣x+6或﹣3x+8;
的结果为﹣x+6或﹣3x+8;
(3)结论:不变,BC﹣AB=2.
理由:
经过t秒,点A向左运动了t个单位长度,点B向右运动了2t个单位长度,点C向右运动了5t个单位长度,而开始运动之前,AB=1-(-1)=2,BC=5-1=4,
∴运动t秒后,AB=t+2t+2=3t+2,BC=5t-2t+4=3t+4,
∵AB=3t+2,BC=3t+4
∴BC﹣AB=(3t+4)-(3t+2)=2
∴BC﹣AB的值不变,BC﹣AB=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
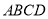 中,
中,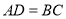 ,
,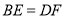 ,
, ,
,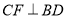 ,垂足分别为
,垂足分别为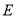 、
、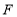 .
.
(1)求证:
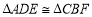 ;
;(2)若
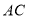 与
与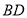 相交于点
相交于点 ,求证:
,求证: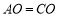 .
. -
科目: 来源: 题型:
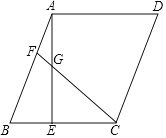
查看答案和解析>>【题目】在ABCD中,AE⊥BC于点E,F为AB边上一点,连接CF,交AE于点G,CF=CB=AE.
(1)若AB
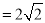 ,BC
,BC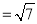 ,求CE的长;
,求CE的长;(2)求证:BE=CG﹣AG.
-
科目: 来源: 题型:
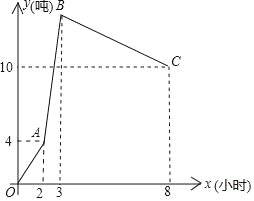
查看答案和解析>>【题目】某仓库有甲、乙、丙三辆运货车,每辆车只负责进货或出货,丙车每小时的运输量最多,乙车每小时的运输量最少,乙车每小时运6吨,如图是甲、乙、丙三辆运输车开始工作后,仓库的库存量y(吨)与工作时间x(小时)之间函数图象,其中OA段只有甲、丙两车参与运输,AB段只有乙、丙两车参与运输,BC段只有甲、乙两车参与运输.
(1)在甲、乙、丙三辆车中,出货车是 .(直接写出答案)
(2)甲车和丙车每小时各运输多少吨?
(3)由于仓库接到临时通知,要求三车在8小时后同时开始工作,但丙车在运送10吨货物后出现故障而退出,问:8小时后,甲、乙两车又工作了几小时,使仓库的库存量为8吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=a(x+3)(x﹣1)(a≠0),与x轴从左至右依次相交于A、B两点,与y轴相交于点C,经过点A的直线y=﹣
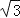 x+b与抛物线的另一个交点为D.
x+b与抛物线的另一个交点为D.(1)若点D的横坐标为2,求抛物线的函数解析式;
(2)若在第三象限内的抛物线上有点P,使得以A、B、P为顶点的三角形与△ABC相似,求点P的坐标;
(3)在(1)的条件下,设点E是线段AD上的一点(不含端点),连接BE.一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒
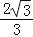 个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?
个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?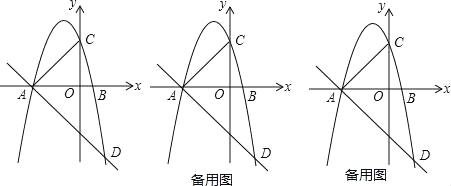
-
科目: 来源: 题型:
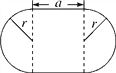
查看答案和解析>>【题目】一个花坛的形状如图所示,它的两端是半径相等的半圆,求:
(1)花坛的周长l;
(2)花坛的面积S;
(3)若a=8m,r=5m,求此时花坛的周长及面积(π取3.14).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班级选派甲、乙两位同学参加学校的跳远比赛,体育老师对他们的5次训练成绩进行了整理,并绘制了不完整的统计图,如图所示,请根据图中信息,解答下列问题:
甲、乙两人跳远成绩统计表:
第1次
第2次
第3次
第4次
第5次
甲成绩/厘米
588
597
608
610
597
乙成绩/厘米
613
618
580
a
618
根据以上信息,请解答下列问题:
(1)a= ;
(2)请完成图中表示甲成绩变化情况的折线;
(3)通过计算,补充完整下面的统计分析表;
运动员
最好成绩
平均数
众数
方差
甲
597
41.2
乙
618
600.6
378.24
(4)请依据(3)中所统计的数据分析,甲、乙两位同学的训练成绩各有什么特点.

相关试题

