【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,则图中阴影部分的面积为( )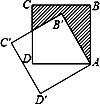
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】C
【解析】设B′C′与CD的交点为E,连接AE,利用“HL”证明Rt△AB′E和Rt△ADE全等,根据全等三角形对应角相等∠DAE=∠B′AE,再根据旋转角求出∠DAB′=60°,然后求出∠DAE=30°,再解直角三角形求出DE,然后根据阴影部分的面积=正方形ABCD的面积﹣四边形ADEB′的面积,列式计算即可得解.
如图,设B′C′与CD的交点为E,连接AE,
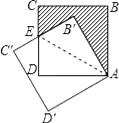
在Rt△AB′E和Rt△ADE中, ![]() ,
,
∴Rt△AB′E≌Rt△ADE(HL),
∴∠DAE=∠B′AE,
∵旋转角为30°,
∴∠DAB′=60°,
∴∠DAE= ![]() ×60°=30°,
×60°=30°,
∴DE=1× ![]() =
= ![]() ,
,
∴阴影部分的面积=1×1﹣2×( ![]() ×1×
×1× ![]() )=1﹣
)=1﹣ ![]() .
.
故答案为:C.
利用“HL”证明Rt△AB′E和Rt△ADE全等,根据全等三角形对应角相等∠DAE=∠B′AE,再根据旋转角求出∠DAB′=60°,然后求出∠DAE=30°,再解直角三角形求出DE,然后根据阴影部分的面积=正方形ABCD的面积﹣四边形ADEB′的面积,列式计算即可得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°,连接CE.
(1)求证:△ABD≌△ACE;
(2)求证:CE平分∠ACF;
(3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则点B3的坐标是_____;点B2018的坐标是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】农夫将苹果树种在正方形的果园内.为了保护苹果树不怕风吹,他在苹果树的周围种针叶树.在下图里,你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律:当n为某一个数值时,苹果树数量会等于针叶树数量,则n为( )

A.6
B.8
C.12
D.16 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E,F分别是矩形ABCD的边BC和CD上的点,其中AB=3
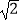 ,BC=3
,BC=3 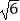 ,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为 .
,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为 . 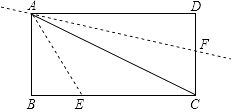
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC,BD为圆O的两条互相垂直的直径,动点P从圆心O出发,沿O→C→D→O的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,那么表示y与t之间函数关系的图象大致为( )
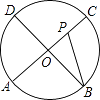
A.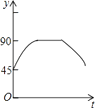
B.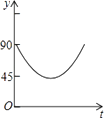
C.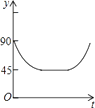
D.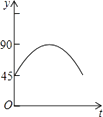
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的,该市自来水收费价格见价目表.
价目表
每月水用量
单价
不超出
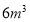 的部分
的部分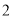 元/
元/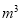
超出
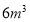 不超出
不超出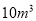 的部分
的部分 元/
元/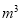
超出
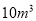 的部分
的部分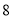 元/
元/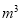
注:水费按月结算.
若某户居民
 月份用水
月份用水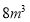 ,则应收水费:
,则应收水费: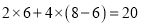 元.
元.(1)若该户居民
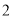 月份用水
月份用水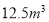 ,则应收水费_______元;
,则应收水费_______元;(2)若该户居民
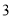 、
、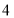 月份共用水
月份共用水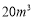 (
(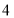 月份用水量超过
月份用水量超过 月份),共交水费
月份),共交水费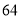 元,则该户居民
元,则该户居民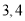 月份各用水多少立方米?
月份各用水多少立方米?
相关试题

