【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则点B3的坐标是_____;点B2018的坐标是_____.

参考答案:
【答案】(7,4) (22018﹣1,22017)
【解析】
首先求得直线的解析式,分别求得B1,B2,B3…的坐标,可以得到一定的规律,据此即可求解.
解:∵B1的坐标为(1,1),点B2的坐标为(3,2),
∴正方形A1B1C1O1边长为1,正方形A2B2C2C1边长为2,

∴A1的坐标是(0,1),A2的坐标是:(1,2),
代入y=kx+b得![]() ,
,
解得:![]() .
.
则直线的解析式是:y=x+1.
∵点B1的坐标为(1,1),点B2的坐标为(3,2),
∴点B3的坐标为(7,4),…,
∴Bn的横坐标是:2n-1,纵坐标是:2n-1.
Bn的坐标是(2n-1,2n-1)
∴B2018的坐标是(22018-1,22017).
故答案为:(7,4),(22018-1,22017).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为( )

A.
B.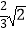
C.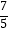
D.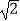
-
科目: 来源: 题型:
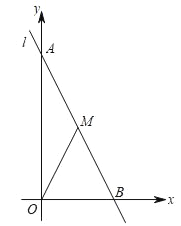
查看答案和解析>>【题目】如图,已知在平面直角坐标中,直线l:y=﹣2x+6分别交两坐标于A、B两点,M是级段AB上一个动点,设点M的横坐标为x,△OMB的面积为S.
(1)写出S与x的函数关系式;
(2)当△OMB的面积是△OAB面积的
 时,求点M的坐标;
时,求点M的坐标;(3)当△OMB是以OB为底的等腰三角形,求它的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°,连接CE.
(1)求证:△ABD≌△ACE;
(2)求证:CE平分∠ACF;
(3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】农夫将苹果树种在正方形的果园内.为了保护苹果树不怕风吹,他在苹果树的周围种针叶树.在下图里,你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律:当n为某一个数值时,苹果树数量会等于针叶树数量,则n为( )

A.6
B.8
C.12
D.16 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,则图中阴影部分的面积为( )
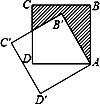
A.
B.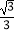
C.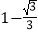
D.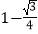
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E,F分别是矩形ABCD的边BC和CD上的点,其中AB=3
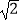 ,BC=3
,BC=3 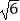 ,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为 .
,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为 . 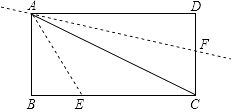
相关试题

