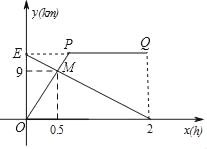
【题目】甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图的折线OPQ和线段EF,分别表示甲、乙两人与A地的距离y甲、y乙与他们所行时间x(h)之间的函数关系,且OP与EF相交于点M.
(1)求线段OP对应的y甲与x的函数关系式(不必注明自变量x的取值范围);
(2)求y乙与x的函数关系式以及A,B两地之间的距离;
(3)请从A,B两题中任选一题作答,我选择 题.
A.直接写出经过多少小时,甲、乙两人相距3km;
B.设甲、乙两人的距离为s(km),直接写出s与x的函数关系式,并注明x的取值范围.
参考答案:
【答案】(1)线段OP对应的函数解析式为y甲=18x;(2)A、B两地的距离是12km;(3)见解析.
【解析】
(1)根据函数图象中的数据可以求得相应的函数解析式;
(2)根据图象中的数据可以求得相应的函数解析式和AB两地的距离;
(3)任选一题,然后根据(1)和(2)中的函数解析式即可解答本题.
解:(1)设线段OP对应的函数解析式为y甲=kx,
9=0.5k,得k=18,
∴线段OP对应的函数解析式为y甲=18x;
(2)设y乙与x的函数关系式是y乙=mx+n,
![]() ,得
,得![]() ,
,
即y乙与x的函数关系式是y乙=﹣6x+12,
当x=0时,y乙=12,
∴A、B两地的距离是12km;
(3)请从A,B两题中任选一题作答,我选择B题,
故答案为:B,
B题:当0≤x≤0.5时,s=(﹣6x+12)﹣18x=﹣24x+12,
甲到达B地用的时间为:12÷(9÷0.5)=![]() 小时,
小时,
当0.5<x≤![]() 时,s=18x﹣(﹣6x+12)=24x﹣12,
时,s=18x﹣(﹣6x+12)=24x﹣12,
当![]() <x≤2时,s=12﹣(﹣6x+12)=6x.
<x≤2时,s=12﹣(﹣6x+12)=6x.
补充:若选A,解答如下,
当0≤x≤0.5时,(﹣6x+12)﹣18x=3,解得,x=![]() ,
,
当0.5<x≤![]() 时,18x﹣(﹣6x+12)=3,得x=
时,18x﹣(﹣6x+12)=3,得x=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校招聘一名数学老师,对应聘者分别进行了教学能力、科研能力和组织能力三项测试,其中甲、乙两名应聘者的成绩如右表:(单位:分)
教学能力
科研能力
组织能力
甲
81
85
86
乙
92
80
74
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将被录用?
(2)根据实际需要,学校将教学、科研和组织能力三项测试得分按 5:3:2 的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,G、F分别为AD、BC的中点,将纸片折叠,使D点落在GF上,得到△HAE , 再过H点折叠纸片,使B点落在直线AB上,折痕为PQ.连接AF、EF , 已知HE=HF.下列结论:①△MEH为等边三角形;②AE⊥EF;③△PHE∽△HAE;④
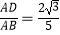 ,
, 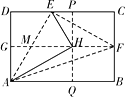
其中正确的结论是
A.①②③
B.①②④
C.①③④
D.①②③④ -
科目: 来源: 题型:
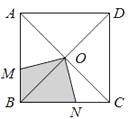
查看答案和解析>>【题目】如图,一只小猫被关在正方形ABCD区域内,点O是对角线的交点,∠MON=90°,OM、ON分别交线段AB、BC于M、N两点,则小猫停留在阴影区域的概率为.
-
科目: 来源: 题型:
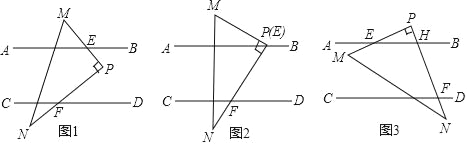
查看答案和解析>>【题目】问题情境:已知:如图1,直线AB∥CD,现将直角三角板△PMN放入图中,其中∠MPN=90°,点P始终在直线MN右侧.PM交AB于点E,PN交CD于点F,试探究:∠PFD与∠AEM的数量关系.
(1)特例如图2,当点P在直线AB上(即点E与点P重合)时,直接写出∠PFD与∠AEM的数量关系,不必证明;
(2)类比探究:如图1,当点P在AB与CD之间时,猜想∠PFD与∠AEM的数量关系,并说明理由;
(3)拓展延伸:如图3,当点P在直线AB的上方时,PN交AB于点H,其他条件不变,猜想∠PFD与∠AEM的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在甲地、乙地分别生产了17台、15台同一种型号的机械设备,现要将这些设备全部运往A、B两市,其中运往A市18台、运往B市14台,从甲地运往A、B两市的费用分别为800元/台和500元/台,从乙地运往A、B两市的费用分别为700元/台和600元/台.设甲地运往A市的设备有x台.
(1)请用x的代数式分别表示甲地运往B市、乙地运往A市、乙地运往B市的设备台数;
(2)求出总运费y(元)与x(台) 的函数关系式,并求出自变量的取值范围;
(3)要使总运费不高于20200元,请你帮助该公司设计调配方案,并写出有哪几种方案,哪种方案总运费最小,最小值是多少?
相关试题

