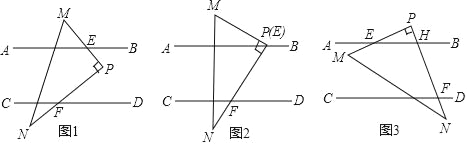
【题目】问题情境:已知:如图1,直线AB∥CD,现将直角三角板△PMN放入图中,其中∠MPN=90°,点P始终在直线MN右侧.PM交AB于点E,PN交CD于点F,试探究:∠PFD与∠AEM的数量关系.
(1)特例如图2,当点P在直线AB上(即点E与点P重合)时,直接写出∠PFD与∠AEM的数量关系,不必证明;
(2)类比探究:如图1,当点P在AB与CD之间时,猜想∠PFD与∠AEM的数量关系,并说明理由;
(3)拓展延伸:如图3,当点P在直线AB的上方时,PN交AB于点H,其他条件不变,猜想∠PFD与∠AEM的数量关系,并说明理由.
参考答案:
【答案】(1)∠PFD+∠AEM=90°,理由见解析;(2)∠PFD+∠AEM=90°,理由见解析;(3)∠PFD﹣∠AEM=90°,理由见解析.
【解析】
(1)根据平行线的性质得到∠PFD=∠APF,结合图形证明;
(2)作PQ∥AB交MN于Q,根据平行线的性质解答;
(3)根据平行线的性质、三角形的外角的性质解答.
解:(1)∠PFD+∠AEM=90°,
理由如下:∵AB∥CD,
∴∠PFD=∠APF,
∵∠APF+∠AEM=90°,
∴∠PFD+∠AEM=90°;
(2)∠PFD+∠AEM=90°,
理由如下:作PQ∥AB交MN于Q,
∵AB∥CD,
∴PQ∥CD,
∴∠AEM=∠QPE,∠PFD=∠QPF,
∵∠QPE+∠QPF=90°,
∴∠PFD+∠AEM=90°;
(3)∠PFD﹣∠AEM=90°,
理由如下:∵AB∥CD,
∴∠PFD=∠PHB,
∵∠PHB﹣∠PEB=90°,∠AEM=∠PEB,
∴∠PHB﹣∠AEM=90°,
∴∠PFD﹣∠AEM=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,G、F分别为AD、BC的中点,将纸片折叠,使D点落在GF上,得到△HAE , 再过H点折叠纸片,使B点落在直线AB上,折痕为PQ.连接AF、EF , 已知HE=HF.下列结论:①△MEH为等边三角形;②AE⊥EF;③△PHE∽△HAE;④
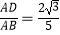 ,
, 
其中正确的结论是
A.①②③
B.①②④
C.①③④
D.①②③④ -
科目: 来源: 题型:
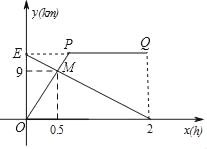
查看答案和解析>>【题目】甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图的折线OPQ和线段EF,分别表示甲、乙两人与A地的距离y甲、y乙与他们所行时间x(h)之间的函数关系,且OP与EF相交于点M.
(1)求线段OP对应的y甲与x的函数关系式(不必注明自变量x的取值范围);
(2)求y乙与x的函数关系式以及A,B两地之间的距离;
(3)请从A,B两题中任选一题作答,我选择 题.
A.直接写出经过多少小时,甲、乙两人相距3km;
B.设甲、乙两人的距离为s(km),直接写出s与x的函数关系式,并注明x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只小猫被关在正方形ABCD区域内,点O是对角线的交点,∠MON=90°,OM、ON分别交线段AB、BC于M、N两点,则小猫停留在阴影区域的概率为.
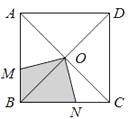
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在甲地、乙地分别生产了17台、15台同一种型号的机械设备,现要将这些设备全部运往A、B两市,其中运往A市18台、运往B市14台,从甲地运往A、B两市的费用分别为800元/台和500元/台,从乙地运往A、B两市的费用分别为700元/台和600元/台.设甲地运往A市的设备有x台.
(1)请用x的代数式分别表示甲地运往B市、乙地运往A市、乙地运往B市的设备台数;
(2)求出总运费y(元)与x(台) 的函数关系式,并求出自变量的取值范围;
(3)要使总运费不高于20200元,请你帮助该公司设计调配方案,并写出有哪几种方案,哪种方案总运费最小,最小值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平面直角坐标系中,直线y=kx+b与x轴交于点A(6,0),与y轴交于点B,与直线y=2x交于点C(a,4).
(1)求点C的坐标及直线AB的表达式;
(2)如图2,在(1)的条件下,过点E作直线l⊥x轴于点E,交直线y=2x于点F,交直线y=kx+b于点G,若点E的坐标是(4,0).
①求△CGF的面积;
②直线l上是否存在点P,使OP+BP的值最小?若存在,直接写出点P的坐标;若不存在,说明理由;
(3)若(2)中的点E是x轴上的一个动点,点E的横坐标为m(m>0),当点E在x轴上运动时,探究下列问题:
当m取何值时,直线l上存在点Q,使得以A,C,Q为顶点的三角形与△AOC全等?请直接写出相应的m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
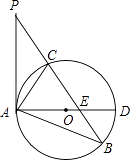
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AGAB=12,求AC的长;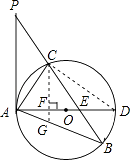
(3)在满足(2)的条件下,若AF:FD=1:2,GF=1,求⊙O的半径及sin∠ACE的值.
相关试题

