【题目】将边长为2的正方形OABC如图放置,O为原点.若∠α=15°,则点B的坐标为 . 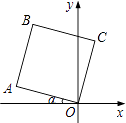
参考答案:
【答案】(﹣ ![]() ,
,![]() )
)
【解析】解:连接OB,过B作BE⊥x轴于E,则∠BEO=90°,
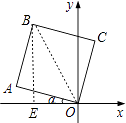
∵四边形OABC是正方形,
∴AB=OA=2,∠A=90°,∠BOA=45°,
由勾股定理得:OB= ![]() =2
=2 ![]() ,
,
∵∠α=15°,∠BOA=45°,
∴∠BOE=45°+15°=60°,
在Rt△BOE中,BE=OB×sin60°=2 ![]() ×
× ![]() =
= ![]() ,OE=OB×cos60°=
,OE=OB×cos60°= ![]() ,
,
∴B的坐标为(﹣ ![]() ,
, ![]() ).
).
所以答案是: ![]()
【考点精析】通过灵活运用勾股定理的概念和正方形的性质,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx+c经过点(0,﹣3),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你确定的b的值是 .
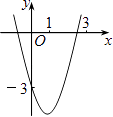
-
科目: 来源: 题型:
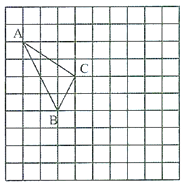
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形△ABC的顶点A、C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请把△ABC先向右移动5个单位,再向下平移3个单位得到△
 ,在图中画出△
,在图中画出△ ;
;(3)求△ABC的面积.
-
科目: 来源: 题型:
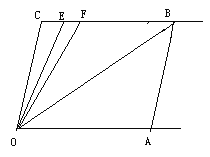
查看答案和解析>>【题目】如图,直线CB∥OA,∠C=∠A=120°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:
 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:设
 (其中
(其中 均为整数),则有
均为整数),则有 .
.∴
 .这样小明就找到了一种把部分
.这样小明就找到了一种把部分 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
当
 均为正整数时,若
均为正整数时,若 ,用含m、n的式子分别表示
,用含m、n的式子分别表示 ,得
,得 = ,
= , = ;
= ;(2)利用所探索的结论,找一组正整数
 ,填空: + =( +
,填空: + =( +  )2;
)2;(3)若
 ,且
,且 均为正整数,求
均为正整数,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知x=
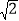 -1,求x2+3x-1的值.(2)已知a=1-
-1,求x2+3x-1的值.(2)已知a=1-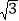 ,b=1+
,b=1+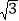 ,求2a2+2b2-3ab-a+b的值.
,求2a2+2b2-3ab-a+b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 把解集在数轴上表示,并求不等式组的整数解.
把解集在数轴上表示,并求不等式组的整数解.
相关试题

