搜索
【题目】如图，已知抛物线y=x2+bx+c经过点（0，﹣3），请你确定一个b的值，使该抛物线与x轴的一个交点在（1，0）和（3，0）之间．你确定的b的值是 ．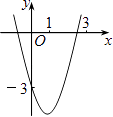 
参考答案：
【答案】1（在﹣2＜b＜2范围内的任何一个数）
【解析】解：把（0，﹣3）代入抛物线的解析式得：c=﹣3，
∴y=x2+bx﹣3，
∵使该抛物线与x轴的一个交点在（1，0）和（3，0）之间，
∴把x=1代入y=x2+bx﹣3得：y=1+b﹣3＜0
把x=3代入y=x2+bx﹣3得：y=9+3b﹣3＞0，
∴﹣2＜b＜2，
即在﹣2＜b＜2范围内的任何一个数都符合，
所以答案是：1（在﹣2＜b＜2范围内的任何一个数）．
【考点精析】认真审题，首先需要了解抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，有若干个整数点(横、纵坐标均为整数)，其顺序按图中方向排列，如(1，0)，(2，0)，(2，1)，(3，1)，(3，0)…… 根据这个规律探索可得，第50个点的坐标为（ ）
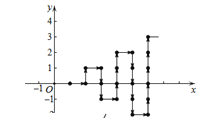
A. (10，－5)B. (10，－1) C. (10，0) D. (10，1）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图1，在平面直角坐标系中，一次函数y＝
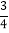x+3交x轴于点A，交y轴于点B，点C是点A关于y轴对称的点，过点C作y轴平行的射线CD，交直线AB与点D，点P是射线CD上的一个动点．(1)求点A，B的坐标．
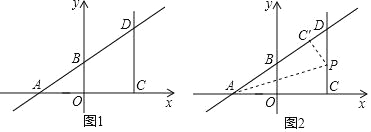
(2)如图2，将△ACP沿着AP翻折，当点C的对应点C′落在直线AB上时，求点P的坐标．
(3)若直线OP与直线AD有交点，不妨设交点为Q(不与点D重合)，连接CQ，是否存在点P，使得S△CPQ＝2S△DPQ，若存在，请求出对应的点Q坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面的证明
如图，FG//CD，∠1=∠3，∠B=50°，求∠BDE的度数.
解：∵FG//CD (已知)
∴∠2=_________（____________________________）
又∵∠1=∠3，
∴∠3=∠2（等量代换）
∴BC//__________（_____________________________）
∴∠B+________=180°（______________________________）
又∵∠B=50°
∴∠BDE=________________.
-
科目： 来源： 题型：
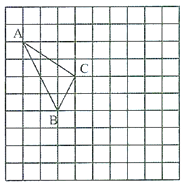
查看答案和解析>>【题目】在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形△ABC的顶点A、C的坐标分别为(－4，5)，(－1，3).
（1）请在如图所示的网格平面内作出平面直角坐标系；
（2）请把△ABC先向右移动5个单位，再向下平移3个单位得到△
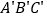，在图中画出△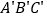；（3）求△ABC的面积.
-
科目： 来源： 题型：
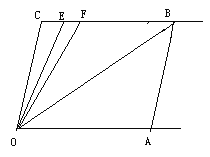
查看答案和解析>>【题目】如图，直线CB∥OA，∠C=∠A=120°，E、F在CB上，且满足∠FOB=∠AOB，OE平分∠COF．
（1）求∠EOB的度数；
（2）若平行移动AB，那么∠OBC：∠OFC的值是否随之发生变化？若变化，找出变化规律或求出变化范围；若不变，求出这个比值；
（3）在平行移动AB的过程中，是否存在某种情况，使∠OEC=∠OBA？若存在，求出其度数；若不存在，说明理由．
-
科目： 来源： 题型：
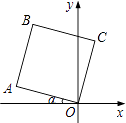
查看答案和解析>>【题目】将边长为2的正方形OABC如图放置，O为原点．若∠α=15°，则点B的坐标为 ．
相关试题
