【题目】解不等式组  把解集在数轴上表示,并求不等式组的整数解.
把解集在数轴上表示,并求不等式组的整数解.
参考答案:
【答案】解: 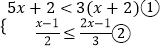 ,
,
解不等式①,得x<2.
解不等式②,得x≥﹣1.
在数轴上表示不等式①,②的解集,

这个不等式组的解集是:﹣1≤x<2.
因此不等式组的整数解为:﹣1、0、1
【解析】先求得两个不等式的解集,然后再依据大小小大中间找确定出不等式组的解集,从而可得到不等式组的整数解,最后,将解集表示在数轴上即可.
【考点精析】本题主要考查了不等式的解集在数轴上的表示和一元一次不等式组的解法的相关知识点,需要掌握不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能正确解答此题.
-
科目: 来源: 题型:
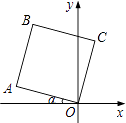
查看答案和解析>>【题目】将边长为2的正方形OABC如图放置,O为原点.若∠α=15°,则点B的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:
 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:设
 (其中
(其中 均为整数),则有
均为整数),则有 .
.∴
 .这样小明就找到了一种把部分
.这样小明就找到了一种把部分 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
当
 均为正整数时,若
均为正整数时,若 ,用含m、n的式子分别表示
,用含m、n的式子分别表示 ,得
,得 = ,
= , = ;
= ;(2)利用所探索的结论,找一组正整数
 ,填空: + =( +
,填空: + =( +  )2;
)2;(3)若
 ,且
,且 均为正整数,求
均为正整数,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知x=
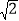 -1,求x2+3x-1的值.(2)已知a=1-
-1,求x2+3x-1的值.(2)已知a=1-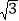 ,b=1+
,b=1+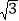 ,求2a2+2b2-3ab-a+b的值.
,求2a2+2b2-3ab-a+b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
-
科目: 来源: 题型:
查看答案和解析>>【题目】在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图.

(1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有名学生.
(2)补全女生等级评定的折线统计图.
(3)根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,回答有关问题:在实数这章中,遇到过
 ,
, ,
, ,
, ,
, 这样的式子,我们把这样的式子叫做二次根式,根号下的数叫做被开方数.如果一个二次根式的被开方数中有的因数能开得尽方,可以利用
这样的式子,我们把这样的式子叫做二次根式,根号下的数叫做被开方数.如果一个二次根式的被开方数中有的因数能开得尽方,可以利用 =
= (a≥0,b≥0);
(a≥0,b≥0); (a≥0,b>0)将这些因数开出来,从而将二次根式化简.当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分母时,这样的二次根式叫做最简二次根式,例如,
(a≥0,b>0)将这些因数开出来,从而将二次根式化简.当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分母时,这样的二次根式叫做最简二次根式,例如,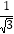 化成最简二次根式是
化成最简二次根式是 ,
, 化成最简二次根式是3
化成最简二次根式是3 ,几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫做同类二次根式,如上面的例子中的
,几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫做同类二次根式,如上面的例子中的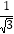 和
和 就是同类二次根式.
就是同类二次根式.(1)请判断下列各式中,哪些是同类二次根式?
 ,
, ,
, ,
, ,
,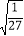 ,
, .
.(2)二次根式中的同类二次根式可以像整式中的同类项一样合并,请计算:
 +
+ -
- -
- +
+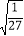 -
- .
.
相关试题

