搜索
【题目】在一个不透明的袋中装有2个黄球和2个红球，它们除颜色外没有其他区别，从袋中任意摸出一个球，然后放加搅匀，再从袋中任意摸一个球，那么两次都摸到黄球的概率是（ ）
A.
B.
C.
D.
参考答案：
【答案】C
【解析】解：如下表：
第一次 | 黄球 | 黄球 | 红球 | 红球 |
黄球 | （黄球，黄球） | （黄球，黄球） | （红球，黄球） | （红球，黄球） |
黄球 | （黄球，黄球） | （黄球，黄球） | （红球，黄球） | （红球，黄球） |
红球 | （黄球，红球） | （黄球，红球） | （红球，红球） | （红球，红球） |
红球 | （黄球，红球） | （黄球，红球） | （红球，红球） | （红球，红球） |
一共有16种等可能的情况，
（黄球，黄球）的一共有4种，则两次都摸到黄球的概率P= 
.
故选：C．
用树状图或列表法，列出所有等可能的情况数量n，找出符合题意的情况数量m，则概率为P= 
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，下列几何体中主视图、左视图、府视图都相同的是（ ）
A.半球
B.圆柱
C.球
D.六棱柱 -
科目： 来源： 题型：
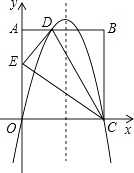
查看答案和解析>>【题目】如图，在矩形ABCD中，AO=10，AB=8，分别以OC、OA所在的直线为x轴，y轴建立平面直角坐标系，点D（3，10）、E（0，6），抛物线y=ax2+bx+c经过O，D，C三点．
（1）求抛物线的解析式；
（2）一动点P从点E出发，沿EC以每秒2个单位长的速度向点C运动，同时动点Q从点C出发，沿CO以每秒1个单位长的速度向点O运动，当点P运动到点C时，两点同时停止运动．设运动时间为t秒，当t为何值时，以P、Q、C为顶点的三角形与△ADE相似？
（3）点N在抛物线对称轴上，点M在抛物线上，是否存在这样的点M与点N，使四边形MENC是平行四边形？若存在，请直接写出点M与点N的坐标（不写求解过程）；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC中，∠ABC=45°，F是高AD和BE的交点，CD=4，则线段DF的长度为（ ）
A.
B.4
C.
D.4
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图，其对称轴为直线x=1，给出下列结论：
①b2-4ac>0；②2a+b=0；③abc>0；④3a+c>0.
则正确的结论个数为（ ）
A.1
B.2
C.3
D.4 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平行四边形ABCD的顶点A、C在双曲线y1=
上，B、D在双曲线y2= 
上，k1=2k2(k1>0)，AB//y轴，S□ABCD=24，则k1=.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在四边形ABCD中，对角线AC、BD相交于点O，设锐角∠AOB=α，将△DOC按逆时针方向旋转得到△D′OC′（0°＜旋转角＜90°）连接AC′、BD′，AC′与BD′相交于点M．
（1）当四边形ABCD为矩形时，如图1．求证：△AOC′≌△BOD′．
（2）当四边形ABCD为平行四边形时，设AC=kBD，如图2．
①猜想此时△AOC′与△BOD′有何关系，证明你的猜想；
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系，并给予证明．
相关试题
