【题目】计算题|1﹣ ![]() |﹣
|﹣ ![]() +2cos30°﹣20170;
+2cos30°﹣20170;
(1)计算:|1﹣ ![]() |﹣
|﹣ ![]() +2cos30°﹣20170;
+2cos30°﹣20170;
(2)解不等式组 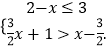 并求其最小整数解.
并求其最小整数解.
参考答案:
【答案】
(1)解:原式= ![]() ﹣1﹣2
﹣1﹣2 ![]() +
+ ![]() ﹣1
﹣1
=﹣2
(2)解: 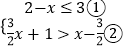
解不等式①得x≥﹣1;
解不等式②得x>﹣5;
不等式组的解集为x≥﹣1;
最小整数解为﹣1
【解析】(1)根据绝对值,特殊角的锐角三角函数值,零指数的意义,二次根式的化简分别进行化简,再按实数的运算方法进行计算即可;(2)解不等式①得x≥﹣1;解不等式②得x>﹣5;然后根据同大取大得出解集,在解集范围内得出最小整数解为﹣1。
【考点精析】解答此题的关键在于理解二次根式的性质与化简的相关知识,掌握1、如果被开方数是分数(包括小数)或分式,先利用商的算数平方根的性质把它写成分式的形式,然后利用分母有理化进行化简.2、如果被开方数是整数或整式,先将他们分解因数或因式,然后把能开得尽方的因数或因式开出来,以及对绝对值的理解,了解正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD对角线BD上截取BE=BC,连接CE并延长交AD于点F,连接AE,过B作BG⊥AE于点G,交AD于点H,则下列结论错误的是( )
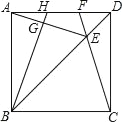
A. AH=DF B. S四边形EFHG=S△DCF+S△AGH
C. ∠AEF=45° D. △ABH≌△DCF
-
科目: 来源: 题型:
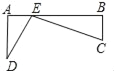
查看答案和解析>>【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为改善洛阳的公共交通状况,洛阳市开始建设地铁系统,如图为某地地铁出站口的示意图,为提高某一段台阶的安全性,决定进行改善,把倾角由45°减至30°,已知原台阶坡面AB的长为5m(BC所在平面为水平面).(结果精确到0.1m,参考数据:
 ≈1.41,
≈1.41, 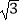 ≈1.73)
≈1.73)
(1)改善后的台阶坡面会加长多少?
(2)改善后的台阶多占多长一段水平地面? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
最喜爱的传统文化项目类型频数分布表项目类型
频数
频率
书法类
18
a
围棋类
14
0.28
喜剧类
8
0.16
国画类
b
0.20
根据以上信息完成下列问题:
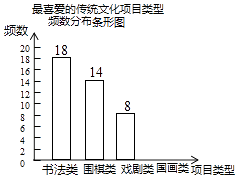
(1)直接写出频数分布表中a的值;
(2)补全频数分布条形图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个运算程序:

例如:根据所给的运算程序可知,当
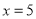 时,
时,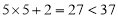 ,再把
,再把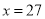 代入,得
代入,得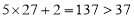 ,则输出的结果为
,则输出的结果为 .
.(1)当
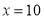 时,输出的结果为_________;当
时,输出的结果为_________;当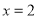 时,输出结果为_________;
时,输出结果为_________;(2)若需要经过两次运算才能输出结果,
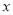 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个长为
 ,宽为
,宽为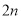 的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.
的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.(1)请用两种不同方法,求图2中阴影部分的面积(不用化简)
方法1:____________________
方法2:____________________
(2)观察图2,写出
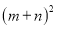 ,
, ,
, 之间的等量关系,并验证;
之间的等量关系,并验证;
(3)根据(2)题中的等量关系,解决如下问题:
①若
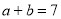 ,
,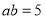 ,求
,求 的值;
的值;②若
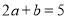 ,
,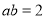 ,求
,求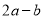 的值.
的值.
相关试题

