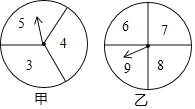
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转运甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
参考答案:
【答案】(1)共有12种等可能性;(2)![]() ;
;![]()
【解析】
试题分析:(1)根据题意列出表格,得出游戏中两数和的所有可能的结果数;
(2)根据(1)得出两数和共有的情况数和其中和小于12的情况、和大于12的情况数,再根据概率公式即可得出答案.
试题解析:(1)根据题意列表如下:
甲 乙 | 6 | 7 | 8 | 9 |
3 | 9 | 10 | 11 | 12 |
4 | 10 | 11 | 12 | 13 |
5 | 11 | 12 | 13 | 14 |
可见,两数和共有12种等可能性;
(2)由(1)可知,两数和共有12种等可能的情况,其中和小于12的情况有6种,和大于12的情况有3种,
∴李燕获胜的概率为![]() ;
;
刘凯获胜的概率为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作与证明:
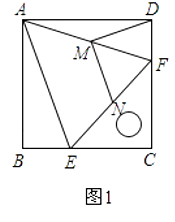
如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.
(1)连接AE,求证:△AEF是等腰三角形;
猜想与发现:
(2)在(1)的条件下,请判断线段MD与MN的关系,得出结论;
结论:DM、MN的关系是:;
拓展与探究:
(3)如图2,将图1中的直角三角板ECF绕点C旋转180°,其他条件不变,则(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.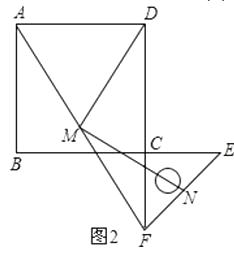
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2﹣2x﹣1=2,则代数式2x2﹣4x的值为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=CD,则∠BEC的度数为( )
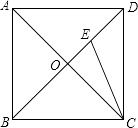
A.22.5°
B.60°
C.67.5°
D.75° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线BD所在直线折叠,点C落在同一平面内,落点记为C′,BC′与AD交于点E,若AB=6,BC=8,则DE的长为( )
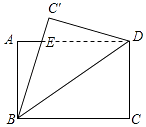
A.6.25
B.6.35
C.6.45
D.6.55 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是假命题的是( )
A. 对顶角相等 B. -4是有理数
C. 内错角相等 D. 同位角相等,两直线平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四组线段中,能组成直角三角形的是( ).
A.a=1,b=2,c=3
B.a=2,b=3,c=4
C.a=2,b=4,c=5
D.a=3,b=4,c=5
相关试题

