【题目】如图,直线L: ![]() 与x轴、y轴分别交于A、B两点,在y轴上有一点
与x轴、y轴分别交于A、B两点,在y轴上有一点
C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动。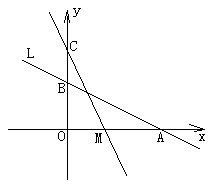
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,并求此时M点的坐标。
参考答案:
【答案】
(1)解: ![]() 与x轴、y轴分别交于A、B两点
与x轴、y轴分别交于A、B两点
令y=0时,x=4,
∴A(4,0)
令x=0时,y=2
∴B(0,2)
(2)解:∵C(0,4),A(4,0),
∴OC=OA=4,
当0![]() t
t![]() 4时,OM=OA-AM=4-t,
4时,OM=OA-AM=4-t,
∴S△COM=![]() ×4×(4-t)=8-2t,
×4×(4-t)=8-2t,
当0![]() 4时,OM=AM-OA=t-4,
4时,OM=AM-OA=t-4,
∴S△COM=![]() ×4×(t-4)=2t-8,
×4×(t-4)=2t-8,
(3)解:分为两种情况:
①当M在OA上时,OB=OM=2,△COM≌△AOB,
∴AM=OA-OM=4-2=2,
∴动点M从A点以每秒1个单位的速度沿x轴向左移动2个单位所需要的时间是2秒钟,
∴M(2,0);
②当M在OA延长线上时,OB=OM=2,
∴M(-2,0),
此时需要的时间t=【4-(-2)】÷1=6秒,
∴M点坐标为M(2,0)或M(-2,0).
【解析】(1)由直线L的函数解析式,令y=0求A点坐标,x=0求B点坐标;
(2)由面积公式S=![]() ×|OM|×|OC|,求出S与t之间的函数关系式;
×|OM|×|OC|,求出S与t之间的函数关系式;
(3)若△COM≌△AOB,OM=OA,则t时间内移动了AM,可算出t值,并得到M坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O
 C
C  B
B  A运动,点P的运动时间为t秒.
A运动,点P的运动时间为t秒.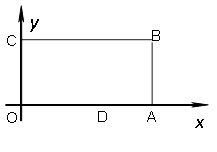
(1)当t=5时, P点坐标为( , )
(2)当t>4时,OP+PD有最小值吗?如果有,请算出该最小值,如果没有,请说明理由。
(3)当t为何值时,△ODP是腰长为5的等腰三角形?(直接写出t的值)。 -
科目: 来源: 题型:
查看答案和解析>>【题目】若α、β是方程x2+2x﹣2017=0的两个实数根,则α2+3α+β的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件为必然事件的是( )
A.小王参加本次数学考试,成绩是150分
B.某射击运动员射靶一次,正中靶心
C.打开电视机,CCTV第一套节目正在播放新闻
D.口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣4,0),点B的坐标是(0,b)(b>0),点P是直线AB上的一个动点,记点P关于y轴对称的点为P′.
(1)当b=3时(如图1),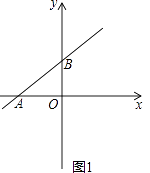
①求直线AB的函数表达式.
(2)②在x轴上找一点Q(点O除外),使△APQ与△AOB全等,直接写出点Q的所有坐标
(3)若点P在第一象限(如图2),设点P的横坐标为a,作PC⊥x轴于点C,连结AP′,CP′.当△ACP′是以点P′为直角顶点的等腰直角三角形时,求出a,b的值.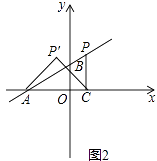
(4)当线段OP′恰好被直线AB垂直平分时(如图3),直接写出b= .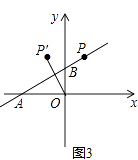
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件是必然发生事件的是( )
A. 打开电视机,正在转播足球比赛
B. 小麦的亩产量一定为1000公斤
C. 在只装有5个红球的袋中摸出1球,是红球
D. 农历十五的晚上一定能看到圆月
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c,其自变量x与函数y的对应值如下表:
x
…
-5
-4
-3
-2
-1
0
…
y
…
4
0
-2
-2
0
4
…
则下列说法正确的是( )
A. 抛物线的开口向下 B. 当x>-3时,y随x的增大而增大
C. 二次函数的最小值是-2 D. 抛物线的对称轴是直线x=-
 .
.
相关试题

