【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O ![]() C
C ![]() B
B ![]() A运动,点P的运动时间为t秒.
A运动,点P的运动时间为t秒.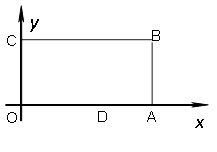
(1)当t=5时, P点坐标为( , )
(2)当t>4时,OP+PD有最小值吗?如果有,请算出该最小值,如果没有,请说明理由。
(3)当t为何值时,△ODP是腰长为5的等腰三角形?(直接写出t的值)。
参考答案:
【答案】
(1)1,4
(2)解:当t>5时,OP+PD有最小值。当点P在BC上时,作点O关于BC为对称轴的对称点O′,此时O′(0,8),连结O′D交BC于P,则OP+PD=O′D= ![]() ,点P在AB上时,OP+PD值均比
,点P在AB上时,OP+PD值均比 ![]() 大,因此OP+PD的最小值是
大,因此OP+PD的最小值是 ![]() 。
。
(3)解:t=6或t=6.5或t=7或t=12
【解析】(1)因为点P从点O出发,以每秒1个单位长度的速度沿O → C → B → A运动,当运动5秒时,因为OC=4,所以点P在线段CB上距点C1个单位长的位置,因此点P的坐标为(1,4);(2)点O关于BC为对称轴的对称点O′的坐标为(0,8),连结O′D交BC于P,根据两点之间线段最短,得到OP+PD的最小值即OP+PD=O′D的值;(3)分①OD=OP=5,②PD=OD=5,③OP=PD=5三种情况讨论,根据题意及勾股定理求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)问题情景:某学校数学学习小组在讨论“随机掷二枚均匀的硬币,得到一正一反的概率是多少”时,小聪说:随机掷二枚均匀的硬币,可以有“二正、一正一反、二反”三种情况,所以,P(一正一反)=
 ;小颖反驳道:这里的“一正一反”实际上含有“一正一反,一反一正”二种情况,所以P(一正一反)=
;小颖反驳道:这里的“一正一反”实际上含有“一正一反,一反一正”二种情况,所以P(一正一反)= .
.⑴ 的说法是正确的.
⑵为验证二人的猜想是否正确,小聪与小颖各做了100次实验,得到如下数据:

计算:小聪与小颖二人得到的“一正一反”的频率分别是多少?从他们的实验中,你能得
到“一正一反”的概率是多少吗?
⑶对概率的研究而言小聪与小颖两位同学的实验说明了什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a是方程x2﹣2x﹣1=0的解,则代数式﹣2a2+4a+2020的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从标号分别为1,2,3,4,5的5张卡片中,随机抽取1张.下列事件中,必然事件是【 】
A.标号小于6 B.标号大于6 C.标号是奇数 D.标号是3
-
科目: 来源: 题型:
查看答案和解析>>【题目】若α、β是方程x2+2x﹣2017=0的两个实数根,则α2+3α+β的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件为必然事件的是( )
A.小王参加本次数学考试,成绩是150分
B.某射击运动员射靶一次,正中靶心
C.打开电视机,CCTV第一套节目正在播放新闻
D.口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线L:
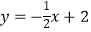 与x轴、y轴分别交于A、B两点,在y轴上有一点
与x轴、y轴分别交于A、B两点,在y轴上有一点
C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动。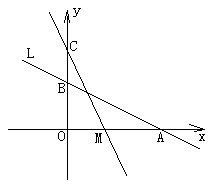
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,并求此时M点的坐标。
相关试题

