【题目】如图,△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,若BD=AD,DE=DC.

(1)求证BF⊥AC;
(2)若AE=2,BE=4,AF=![]() ,求AD的长.
,求AD的长.
参考答案:
【答案】(1)见解析;(2)3.
【解析】
(1)根据SAS推出△BED≌△ACD,根据全等三角形的性质得出∠CAD=∠DBE,根据三角形内角和定理求出∠DBE+∠BED=90°,求出∠AEF+∠CAD=90°,根据三角形内角和定理求出∠AFE=90°,即可得出答案.
(2)由全等三角形的性质得出BE=AC=4,证明△AEF∽△ACD得出![]() ,即可得出结果.
,即可得出结果.
(1)证明:∵AD⊥BC,
∴∠BDE=∠ADC=90°,
在△BED和△ACD中,
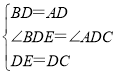 ,
,
∴△BED≌△ACD(SAS),
∴∠CAD=∠DBE,
∵∠BDE=90°,
∴∠DBE+∠BED=90°,
∵∠BED=∠AEF,∠DBE=∠CAD,
∴∠AEF+∠CAD=90°,
∴∠AFE=180°-90°=90°,
∴BF⊥AC.
(2)解:∵△BED≌△ACD,
∴BE=AC=4,
∵∠EAF=∠CAD,∠AFE=∠ADC=90°,
∴△AEF∽△ACD,
∴![]() ,
,
∴AD=2AF=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,D是AB上的点,过点D作DE⊥AB交BC于点F,交AC的延长线于点E,连接CD,∠DCA=∠DAC,则下列结论:①∠DCB=∠B;②CD=
 AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.正确的有______.
AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.正确的有______. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△EBD中,EB=ED,点C在BD上,CE=CD,BE⊥CE,A是CE延长线上一点,EA=EC.
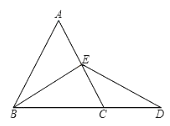
(1)求∠EBC的度数;
(2)求证△ABC为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD.

(1)利用尺规作∠ADC的平分线DE,交BC于点E,在AD上截取AF=AB,连接AE.EF(保留作图痕迹,不写作法);
(2)在(l)的条件下,求证:EC=EF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠ABC+
 .
.
(1)求证:AB=AC;
(2)如图2,点D为AC垂直平分线上一点(点D在AC的右侧),连接BD,∠DBC=30°,∠ABC 的平分线AE交BD于点E;
①求证:△ACD 为等边三角形;
②若AE=nBE,△ABC 的面积记为S△ABC ,△BDC的面积记为S△BDC,则
 的值为_____.
的值为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+x+3的顶点为P,与y轴交于点A,若向右平移4个单位,向下平移4个单位,则抛物线上PA段扫过的区域(阴影部分)的面积为__________.
x2+x+3的顶点为P,与y轴交于点A,若向右平移4个单位,向下平移4个单位,则抛物线上PA段扫过的区域(阴影部分)的面积为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.

(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
相关试题

