【题目】如图,抛物线y=![]() x2+x+3的顶点为P,与y轴交于点A,若向右平移4个单位,向下平移4个单位,则抛物线上PA段扫过的区域(阴影部分)的面积为__________.
x2+x+3的顶点为P,与y轴交于点A,若向右平移4个单位,向下平移4个单位,则抛物线上PA段扫过的区域(阴影部分)的面积为__________.

参考答案:
【答案】12
【解析】
根据题意求得A,P的坐标,再根据平移的性质得到四边形A PP′A′为平行四边形,以及A′,P的坐标,然后求得AD,PP′的长,再求出面积即可.
如图,连接AP,AP′,过点A作AD⊥PP′于D点,

由题意可得,四边形APP′A′为平行四边形,
将x=0代入函数得y=3,
∴点A的坐标为(0,3),
又∵抛物线y=![]() x2+x+3=
x2+x+3=![]() (x2+4x+4)+2=
(x2+4x+4)+2=![]() (x+2)2+2,
(x+2)2+2,
∴顶点P的坐标为(﹣2,2),
∵将抛物线向右平移4个单位,向下平移4个单位,
∴点A′(4,﹣1),点P′(2,﹣2),
∴PP′=![]() =4
=4![]() ,A0=3,∠AOP=45°,
,A0=3,∠AOP=45°,
∴△AOD为等腰直角三角形,
∴AD=OD,
在Rt△AOD中,AD2+OD2=9,即2AD2=9,
∴AD=![]() ,
,
则抛物线上PA段扫过的区域(阴影部分)的面积为4![]() ×
×![]() =12.
=12.
故答案为12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD.

(1)利用尺规作∠ADC的平分线DE,交BC于点E,在AD上截取AF=AB,连接AE.EF(保留作图痕迹,不写作法);
(2)在(l)的条件下,求证:EC=EF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,若BD=AD,DE=DC.

(1)求证BF⊥AC;
(2)若AE=2,BE=4,AF=
 ,求AD的长.
,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠ABC+
 .
.
(1)求证:AB=AC;
(2)如图2,点D为AC垂直平分线上一点(点D在AC的右侧),连接BD,∠DBC=30°,∠ABC 的平分线AE交BD于点E;
①求证:△ACD 为等边三角形;
②若AE=nBE,△ABC 的面积记为S△ABC ,△BDC的面积记为S△BDC,则
 的值为_____.
的值为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.

(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用直尺和圆规作一个角∠A′O′B′,等于已知角∠AOB,能得出∠A′O′B′=∠AOB的依据是( )

A.SASB.ASAC.AASD.SSS
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
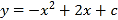 与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).
与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).(1)求该抛物线的解析式及顶点M的坐标;
(2)求△EMF与△BNF的面积之比.

相关试题

