【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.

(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
参考答案:
【答案】(1)x=1或x=3是方程ax2+bx+c=0的两个根;(2)l<x<3;(3)当x>2时,y随x的增大而减小;(4)k<2.
【解析】试题分析:(1)观察图形可以看出抛物线与x轴交于(1,0)和(3,0),即可解题
(2)根据抛物线y=ax2+bx+c,求得y>0的x取值范围即可解题;
(3)图中可以看出抛物线对称轴,即可解题;
(3)易求得抛物线解析式,根据方程△>0即可解题.
试题解析:(1)图中可以看出抛物线与x轴交于(1,0)和(3,0),
∴方程ax2+bx+c=0的两个根为x=1或x=3;
(2)不等式ax2+bx+c>0时,通过图中可以看出:当1<x<3时,y的值>0,
∴不等式ax2+bx+c>0的解集为(1,3);
(3)图中可以看出对称轴为x=2,
∴当x>2时,y随x的增大而减小;
(4)∵抛物线y=ax2+bx+c经过(1,0),(2,2),(3,0),
∴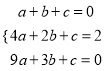 ,
,
解得:a=2,b=8,c=6,
∴2x2+8x6=k,移项得2x2+8x6k=0,
△=644(2)(6k)>0,
整理得:168k>0,
∴k<2时,方程ax2+bx+c=k有2个相等的实数根。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在四边形ABCD中,AB=AD. ∠B+∠ADC=180°,点E,F分别在四边形ABCD的边BC,CD上,∠EAF=
 ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.
图1 图2 图3
(1)思路梳理
将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合.由∠B+∠ADC=180°,得∠FDG=180°,即点F,D,G三点共线. 易证△AFG
 ,故EF,BE,DF之间的数量关系为 ;
,故EF,BE,DF之间的数量关系为 ;(2)类比引申
如图2,在图1的条件下,若点E,F由原来的位置分别变到四边形ABCD的边CB,DC的延长线上,∠EAF=
 ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°. 若BD=1,EC=2,则DE的长为 .
-
科目: 来源: 题型:
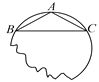
查看答案和解析>>【题目】如图,要把残破的轮片复制完整,已知弧上的三点A、B、C.
(1)用尺规作图法找出
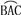 所在圆的圆心(保留作图痕迹,不写作法);
所在圆的圆心(保留作图痕迹,不写作法);(2)设△ABC是等腰三角形,底边BC=8cm,腰AB=5cm,求圆片的半径R.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以下各图都是由同样大小的图形①按一定规律组成,其中第①个图形中共有1个完整菱形,第②个图形中共有5个完整菱形,第③个图形中共有13个完整菱形,…,则第⑦个图形中完整菱形的个数为( )

A. 83B. 84C. 85D. 86
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学拓展课上,九(1)班同学根据学习函数的经验,对新函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下:
【初步尝试】求二次函数y=x2﹣2x的顶点坐标及与x轴的交点坐标;
【类比探究】当函数y=x2﹣2|x|时,自变量x的取值范围是全体实数,下表为y与x的几组对应值.
x
…
﹣3
﹣

﹣2
﹣1
0
1
2

3
…
y
…
3
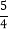
0
﹣1
0
﹣1
0
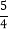
3
…
①根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请你画出该函数图象的另一部分;
②根据画出的函数图象,写出该函数的两条性质.
【深入探究】若点M(m,y1)在图象上,且y1≤0,若点N(m+k,y2)也在图象上,且满足y2≥3恒成立,求k的取值范围.
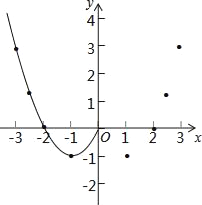
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD.求证:EG∥FH.

请完成以下证明过程:
证明:∵AB∥CD(已知)
∴∠AEF=∠EFD(__________________)
∵EG平分∠AEF,FH平分∠EFD(__________)
∴∠___=
 ∠AEF,∠___=
∠AEF,∠___=  ∠EFD(____________)
∠EFD(____________)∴∠_____=∠______(等量代换)
∴EG∥FH(__________________).
-
科目: 来源: 题型:
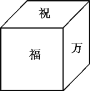
查看答案和解析>>【题目】一个正方体礼盒如图所示,六个面分别写有“祝”“福”“祖”“国”“万”“岁”,其中“祝”的对面是“祖”,“万”的对面是“岁”,则它的表面展开图可能是( )
A.
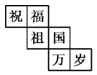 B.
B. 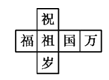 C.
C. 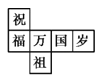 D.
D. 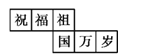
相关试题

