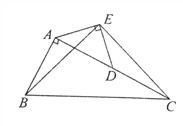
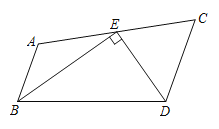
【题目】如图在Rt△ABC中,∠BAC=90 o,AC=2AB,点D是AC的中点,将一块锐角为45 o的直角三角板如图放置,使三角板斜边的两个端点分别与A,D重合,连接BE,EC。试猜想线段BE和EC的数量及位置关系,并证明你的猜想。
参考答案:
【答案】BE=EC且BE⊥EC,证明见解析.
【解析】试题分析:数量关系为:BE=EC,位置关系是:BE⊥EC;利用直角三角形斜边上的中线等于斜边的一半,以及等腰直角三角形的性质,即可证得:△EAB≌△EDC即可证明.
试题解析:BE=EC BE⊥EC
证明∵AC=2AB,点D是AC的中点
∴AB=AD=CD
∵∠EAD=∠EDA=45°
∴∠EAB=∠EDC=135°
∵EA=ED
∴△EAB≌△EDC
∴∠AEB=∠DEC,EB=EC
∴∠BEC=∠AED=90°
∴BE=EC,BE⊥EC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,△ABC的顶点A(-3,0)、B(0,3),AD⊥BC交BC于D点,交y轴正半轴于点E(0,t)
(1)当t=1时,求C点的坐标;
(2)如图2,求∠ADO的度数;
(3)如图3,已知点P(0,2),若PQ⊥PC,PQ=PC,求Q的坐标(用含t的式子表示).
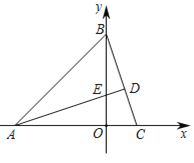
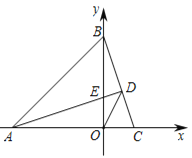
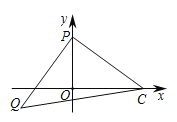
图1 图2 图3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某专业户要出售300只羊,现在市场上羊的价格为每千克11元,为了估计这300只羊能卖多少钱,试问:(1)对于上述问题你认为是用普查好还是抽样调查好?
(2)该专业户从中随机抽取了5只羊,称得它们的重量如下:(单位:千克)
26 31 32 36 37
①在这个问题中,总体、个体和样本各是什么?
②通过上述数据,你能估计出这300只羊约能卖得多少元钱吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据,如图是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:

(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调查人数的百分比是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+2x﹣3,用配方法化为y=a(x﹣h)2+k的形式,结果是( )
A.y=﹣(x﹣1)2﹣2
B.y=﹣(x﹣1)2+2
C.y=﹣(x﹣1)2+4
D.y=﹣(x+1)2﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣4x+m的顶点在x轴上,则m的值等于( )
A.2
B.4
C.6
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BE平分∠ABD,DE平分∠CDB相交于AC上一点E,∠BED=90°,求证:AB∥CD.
相关试题

