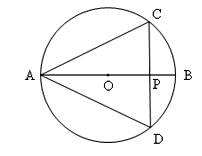
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若AB=2,AC=![]() .
.
(1)求∠A的度数.
(2)求弧CBD的长.
(3)求弓形CBD的面积.
参考答案:
【答案】(1)∠A=30°;(2)![]() ;(3)
;(3)![]() -
-![]() .
.
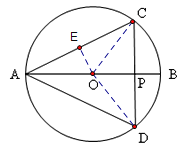
【解析】试题分析:(1)过O作OE⊥AC,由垂径定理可得AE的长,再用三角函数即可求得∠A的度数;
(2)由∠A得度数得出对应圆心角∠COB的度数,由垂径定理得∠DOB=∠COB,由此得到∠COD的度数,用弧长公式即可求出弧长;
(3)由公式:弓形CBD的面积=扇形COD的面积△COD的面积,即可求出弓形面积.
试题解析:(1)过O作OE⊥AC,
![]() ,
,
![]()
在Rt△AEO中, ![]()
![]()
(2)连结OC,OD, ![]()
![]()
∵AB是⊙O的直径,弦CD⊥AB,
∴![]() =
=![]() ,
,
![]()
![]()
∵AB=2,
![]()
∴![]() 的长=
的长=![]() ;
;
(3) ![]() OP⊥CD,
OP⊥CD,
![]()
∵OC=1,
![]()
![]() ,
,
∴弓形CBD的面积=扇形COD的面积△COD的面积![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形
 中,
中,  ∥
∥ ,∠
,∠ =90°,
=90°, =28cm,
=28cm,  =24cm,
=24cm, 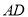 =4cm,点
=4cm,点 从点
从点 出发,以1cm/s的速度向点
出发,以1cm/s的速度向点 运动,点
运动,点 从点
从点 同时出发,以2cm/s的速度向点
同时出发,以2cm/s的速度向点 运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动。则四边
运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动。则四边 的面积
的面积 (cm2)与两动点运动的时间
(cm2)与两动点运动的时间 (s)的函数图象大致是( )
(s)的函数图象大致是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】从2018年4月1日起厦门市实行新的自来水收费阶梯水价收费标准如下表.

备注:1.每月居民用水缴费包括实际用水的水费和污水处理费两部分.2.以上表中的价格均不包括1元/吨的污水处理费.
(1)某用户12月份用水量为20吨,则该用户12月份应缴水费是多少?
(2)若某用户的月用水量为m吨,请用含m的式子表示该用户月所缴水费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形角平分线交点或三角形内切圆的圆心都称为三角形的内心.按此说法,四边形的四个角平分线交于一点,我们也称为“四边形的内心”.
(1)试举出一个有内心的四边形.
(2)探究:对于任意四边形ABCD,如果有内心,则四边形的边长具备何种条件?为什么?
(3)探究:腰长为
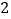 的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?
的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?(4)问题(3)中,O是四边形ABDE内心,且四边形ABDE是等腰梯形,求DE的长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.
(1)求证:DE是⊙O的切线;
(2)若AB=6,AE=
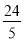 ,求BD和BC的长.
,求BD和BC的长.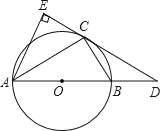
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点O在边AB上,∠AOC=∠BOD.求证:AO=OB.
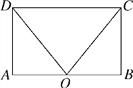
相关试题

