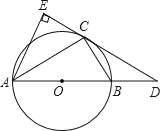
【题目】如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.
(1)求证:DE是⊙O的切线;
(2)若AB=6,AE=![]() ,求BD和BC的长.
,求BD和BC的长.
参考答案:
【答案】(1)证明见解析;(2)BD=2;BC=![]() .
.
【解析】试题分析:(1)要证DE是⊙O的切线,只要连接OC,再证∠DCO=90°即可.
(2)已知两边长,求其它边的长,可以证明三角形相似,由相似三角形对应边成比例来求.
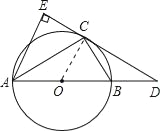
试题解析:解:(1)连接OC.∵AE⊥DC,∴∠E=90°.∵AC平分∠EAB,∴∠EAC=∠BAC.
又∵OA=OC,∴∠ACO=∠BAC,∴∠EAC=∠ACO,∴OC∥AE,∴∠OCD=∠E=90°,∴DC是⊙O的切线.
(2)∵∠D=∠D,∠E=∠OCD=90°,∴△DCO∽△DEA,∴ ![]() ,∴
,∴![]() ,∴
,∴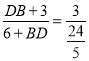 ,∴BD=2.∵AB是⊙O的直径,∴∠ACB=90°,∴∠E=∠ACB=90°.∵∠EAC=∠BAC,∴Rt△EAC∽Rt△CAB,∴
,∴BD=2.∵AB是⊙O的直径,∴∠ACB=90°,∴∠E=∠ACB=90°.∵∠EAC=∠BAC,∴Rt△EAC∽Rt△CAB,∴![]() ,∴
,∴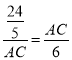 ,∴AC2=
,∴AC2=![]() .由勾股定理得:BC=
.由勾股定理得:BC=![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从2018年4月1日起厦门市实行新的自来水收费阶梯水价收费标准如下表.

备注:1.每月居民用水缴费包括实际用水的水费和污水处理费两部分.2.以上表中的价格均不包括1元/吨的污水处理费.
(1)某用户12月份用水量为20吨,则该用户12月份应缴水费是多少?
(2)若某用户的月用水量为m吨,请用含m的式子表示该用户月所缴水费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形角平分线交点或三角形内切圆的圆心都称为三角形的内心.按此说法,四边形的四个角平分线交于一点,我们也称为“四边形的内心”.
(1)试举出一个有内心的四边形.
(2)探究:对于任意四边形ABCD,如果有内心,则四边形的边长具备何种条件?为什么?
(3)探究:腰长为
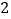 的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?
的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?(4)问题(3)中,O是四边形ABDE内心,且四边形ABDE是等腰梯形,求DE的长?
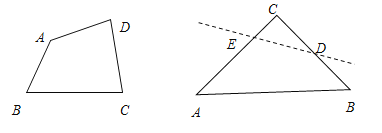
-
科目: 来源: 题型:
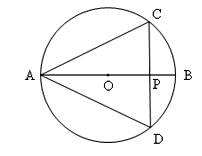
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若AB=2,AC=
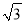 .
.(1)求∠A的度数.
(2)求弧CBD的长.
(3)求弓形CBD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是________.

-
科目: 来源: 题型:
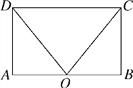
查看答案和解析>>【题目】如图,在矩形ABCD中,点O在边AB上,∠AOC=∠BOD.求证:AO=OB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在黄州服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为20元,并且每周(7天)涨价2元,从第6周开始保持30元的价格平稳销售;从第12周开始,当季节即将过去时,平均每周减价2元,直到第16周周末,该服装不再销售.
(1)试建立销售价y与周次x之间的函数关系式;
(2)若这种时装每件进价Z与周次x次之间的关系为Z=﹣0.125(x﹣8)2+12,1≤x≤16,且x为整数,试问该服装第几周出售时,每件销售利润最大?最大利润为多少?
相关试题

