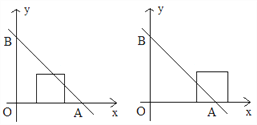
【题目】如图,直线y=4-x与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于点D。
(1)当点M在AB上运动时,四边形OCMD的周长为________;
(2)当四边形OCMD为正方形时,将正方形OCMD沿着x轴的正方向移动,设平移的距离为a (0<a≤4),在平移过程中:
①当平移距离a=1时, 正方形OCMD与△AOB重叠部分的面积为________;
②当平移距离a是多少时,正方形OCMD的面积被直线AB分成l:3两个部分?

参考答案:
【答案】(1)8;(2)①3.5;②a=![]() 或
或![]()
【解析】试题分析:(1)设点M的横坐标为x,则点M的纵坐标为-x+4(0<x<4,x>0,-x+4>0)根据四边形的周长计算方法计算即可发现,当点M在AB上运动时,四边形OCMD的周长不发生变化,总是等于8.
(2)①当0<a≤2时,S=4-![]() a2=-
a2=-![]() a2+4,并且a=1可求出重叠部分的面积;
a2+4,并且a=1可求出重叠部分的面积;
②当四边形为OCMD为正方形时,先求得正方形的边长,从而可求得正方形的面积,可求得正方形被直线分成的较小的部分的面积为1,然后再证明“较小的部分”为等腰直角三角形,从而可求得该等腰直角三角形的直角边的长度,于是可求得平移的距离.
试题解析:(1)(1)设OC=x,则CM=4-x.
∵MC⊥OA,MD⊥OB,OD⊥OC,
∴四边形OCMD为矩形,
∴四边形OCMD的周长=OD+OC+CM+DM=2(CO+CM)=2(x+4-x)=2×4=8.
(2)①如图( 2 ),当0<a≤2时,S=S四边形O′CMD-S△MEF=4-![]() a2=-
a2=-![]() a2+4,
a2+4,
②∵当四边形为OCMD为正方形时,OC=CM,即x=4-x,解得:x=2,
∴S正方形OCMD的面积=4.
∵正方形OCMD的面积被直线AB分成1:3两个部分,
∴两部分的面积分别为1和3.
当0<a≤2时,如图1所示:
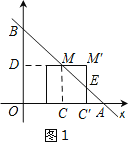
∵直线AB的解析式为y=4-x,
∴∠BAO=45°.
∴△MM′E为等腰直角三角形.
∴MM′=M′E.
∴![]() MM′2=1.
MM′2=1.
∴MM′=![]() ,即a=
,即a=![]()
当2<a<4时,如图2所示:
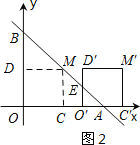
∵∠BAO=45°,
∴△EO′A为等腰直角三角形.
∴EO′=O′A.
∴![]() O′A2=1,解得:O′A=
O′A2=1,解得:O′A=![]() .
.
∵将y=0代入y=4-x得;4-x=0,解得:x=4,
∴OA=4.
∴OO′=4-![]() ,即a=4-
,即a=4-![]() .
.
综上所述,当平移的距离为a=![]() 或a=4
或a=4![]() 时,正方形OCMD的面积被直线AB分成1:3两个部分.
时,正方形OCMD的面积被直线AB分成1:3两个部分.
-
科目: 来源: 题型:
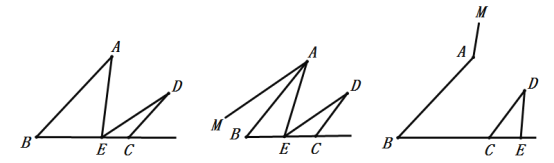
查看答案和解析>>【题目】点D在∠ABC内,点E为边BC上一点,连接DE、CD.
(1)如图1,连接AE,若∠AED=∠A+∠D,求证:AB//CD.
(2)在(1)的结论下,过点A的直线MA//ED.
①如图2,当点E在线段BC上时,猜想并验证∠MAB与∠CDE的数量关系;
②如图3,当点E在线段BC的延长线上时,猜想并验证∠MAB与∠CDE的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:五边形ABCDE中,AB∥CD,BC⊥AB,AB=BC=8,CD=5.
(1)说明∠A,∠E,∠D之间的数量关系;
(2)平移五边形ABCDE,使D点移动到C点,画出平移后的五边形A'B'C'CE',并求出顺次连接A、A'、E'、C、D、E、A各点所围成的图形的面积;
(3)在∠BAE和∠E'CD的内部取一点F,使∠EAF=
 ∠EAB,∠FCE'=
∠EAB,∠FCE'= ∠DCE' ,求∠AFC与∠AED之间的数量关系.
∠DCE' ,求∠AFC与∠AED之间的数量关系.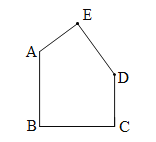
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在8×8的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的格点上.请你在图中找出一点D(仅一个点即可),连结DE,DF,使△DEF与△ABC全等,并给予证明.
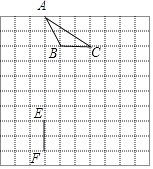
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为 .
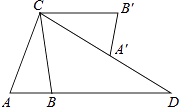
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,且OB=OD.点E在线段OA上,连结BE,DE.给出下列条件:①OC=OE;②AB=AD;③BC⊥CD;④∠CBD=∠EBD.请你从中选择两个条件,使四边形BCDE是菱形,并给予证明.你选择的条件是:(只填写序号).
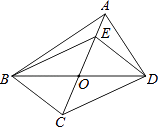
-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆实验外国语学校每年四月初都定期举办体育文化节,初
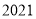 届周华同学为了在本次活动中获得更好的成绩,他让父亲带自己进行了体能训练,他们找了条笔直的跑道
届周华同学为了在本次活动中获得更好的成绩,他让父亲带自己进行了体能训练,他们找了条笔直的跑道 ,两人都从起点
,两人都从起点 出发且一直保持匀速运动,父亲先出发两分钟后周华才出发,两人到达终点
出发且一直保持匀速运动,父亲先出发两分钟后周华才出发,两人到达终点 后均停止运动,周华与父亲之间的距离
后均停止运动,周华与父亲之间的距离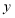 (米)与周华出发的时间
(米)与周华出发的时间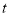 (分)的关系如图所示,当周华到达终点时,父亲离终点的距离为________米.
(分)的关系如图所示,当周华到达终点时,父亲离终点的距离为________米.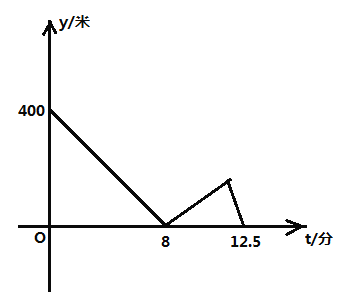
相关试题

