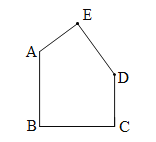
【题目】如图:五边形ABCDE中,AB∥CD,BC⊥AB,AB=BC=8,CD=5.
(1)说明∠A,∠E,∠D之间的数量关系;
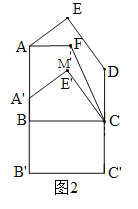
(2)平移五边形ABCDE,使D点移动到C点,画出平移后的五边形A'B'C'CE',并求出顺次连接A、A'、E'、C、D、E、A各点所围成的图形的面积;
(3)在∠BAE和∠E'CD的内部取一点F,使∠EAF=![]() ∠EAB,∠FCE'=
∠EAB,∠FCE'=![]() ∠DCE' ,求∠AFC与∠AED之间的数量关系.
∠DCE' ,求∠AFC与∠AED之间的数量关系.
参考答案:
【答案】(1)∠A+∠E+∠D=360°;(2)40;(3)∠AED=![]() ∠AFC-90°.
∠AFC-90°.
【解析】
(1)根据∠B、∠C的度数和多边形内角和公式即可得出结论;
(2)过E作EM⊥BC于M.由平移的性质可知:E′在EM上,四边形AA'E'E和四边形E'CDE是平行四边形,多边形AA'E'CDE的面积=四边形AA'E'E的面积+四边形E'CDE的面积,根据平行四边形的面积计算公式代入即可得出结论;
(3)过F作FM∥AB.设∠EAF=x,∠E'CF=y,根据平行线的性质可得:x-y=90°-![]() ∠AFC.由(1)得:∠AED=180°-3(x-y),代入即可得出结论.
∠AFC.由(1)得:∠AED=180°-3(x-y),代入即可得出结论.
(1)∵五边形的内角和=(5-2)×180°=540°,∠B=∠C=90°,∴∠A+∠E+∠D=540°-90°-90°=360°;
(2)作图如图1.过E作EM⊥BC于M.由平移的性质可知:E′在EM上,四边形AA'E'E和四边形E'CDE是平行四边形,∴AA'=EE'=DC=5,多边形AA'E'CDE的面积=四边形AA'E'E的面积+四边形E'CDE的面积=AA'×BM+DC×MC=DC×(BM+MC)=DC×BC=5×8=40.
(3)如图2,过F作FM∥AB.设∠EAF=x,∠E'CF=y,则∠FAB=2x,∠EAB=3x,∠FCD=2y,∠E'CD=3y.
∵FM∥AB,AB∥DC,∴∠FAB+∠AFM=180°,FM∥DC,∴∠MFC=∠FCD=2y,∴∠AFC=∠AFM+∠CFM=180°-2x+2y=180°-2(x-y),∴x-y=![]() =90°-
=90°-![]() ∠AFC.
∠AFC.
由(1)得:∠AED=360°-(∠EAB+∠EDC)=360°-(3x+180°-3y)=180°-3(x-y),∴∠AED=180°-3(90°-![]() ∠AFC)=
∠AFC)=![]() ∠AFC-90°.
∠AFC-90°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,正△AOB的边长为2,设直线x=t(0≤t≤2)截这个三角形所得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是( )
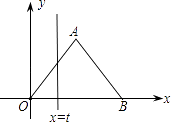
A.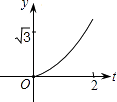
B.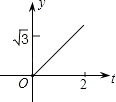
C.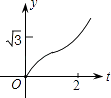
D.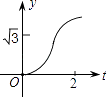
-
科目: 来源: 题型:
查看答案和解析>>【题目】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这种货车的情况如下表:

现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,货主应付运费多少元?
-
科目: 来源: 题型:
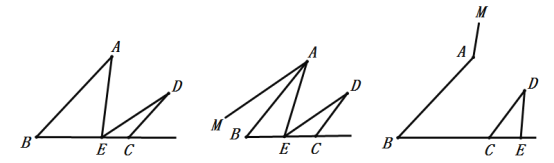
查看答案和解析>>【题目】点D在∠ABC内,点E为边BC上一点,连接DE、CD.
(1)如图1,连接AE,若∠AED=∠A+∠D,求证:AB//CD.
(2)在(1)的结论下,过点A的直线MA//ED.
①如图2,当点E在线段BC上时,猜想并验证∠MAB与∠CDE的数量关系;
②如图3,当点E在线段BC的延长线上时,猜想并验证∠MAB与∠CDE的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在8×8的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的格点上.请你在图中找出一点D(仅一个点即可),连结DE,DF,使△DEF与△ABC全等,并给予证明.
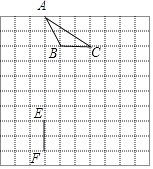
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=4-x与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于点D。
(1)当点M在AB上运动时,四边形OCMD的周长为________;
(2)当四边形OCMD为正方形时,将正方形OCMD沿着x轴的正方向移动,设平移的距离为a (0<a≤4),在平移过程中:
①当平移距离a=1时, 正方形OCMD与△AOB重叠部分的面积为________;
②当平移距离a是多少时,正方形OCMD的面积被直线AB分成l:3两个部分?

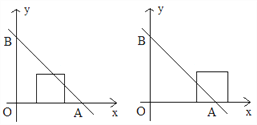
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为 .
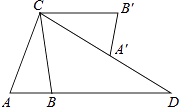
相关试题

