【题目】.在△ABC中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,且
,且![]() 于
于![]() ,
, ![]() 于
于![]() .
.
(1)当直线![]() 绕点
绕点![]() 旋转到图1的位置时,
旋转到图1的位置时, ![]() 的数量关系是_________________ ,并请给出证明过程.
的数量关系是_________________ ,并请给出证明过程.
(2)当直线![]() 绕点
绕点![]() 旋转到图2的位置时,
旋转到图2的位置时, ![]() 的数量关系是_________________ (直接写出结果)。
的数量关系是_________________ (直接写出结果)。
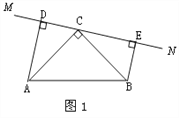

参考答案:
【答案】(1)DE=AD+BE,理由见解析;(2)DE=AD﹣BE
【解析】试题分析:(1)由已知推出∠ADC=∠BEC=90°,因为∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,推出∠DAC=∠BCE,根据AAS可证明△ADC≌△CEB(AAS),依据全等三角形的性质可得到AD=CE,CD=BE,然后由ED=DC+CE可得到问题的答案;
(2)与(1)证法类似可证出∠ACD=∠EBC,能推出△ADC≌△CEB,得到AD=CE,CD=BE,最后由CE=CD+DE可得到问题的答案.
试题解析:证明:(1)∵AD⊥DE,BE⊥DE,∴∠ADC=∠BEC=90°.∵∠ACB=90°,∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,∴∠DAC=∠BCE.在△ADC和△CEB中∵∠CDA=∠BEC,∠DAC=∠ECB,AC=BC,∴△ADC≌△CEB(AAS),∴AD=CE,CD=BE,∵DC+CE=DE,∴AD+BE=DE.
(2)DE=AD﹣BE.理由:
∵BE⊥EC,AD⊥CE,∴∠ADC=∠BEC=90°,∴∠EBC+∠ECB=90°,∵∠ACB=90°,∴∠ECB+∠ACE=90°,∴∠ACD=∠EBC,在△ADC和△CEB中,∵∠ACD=∠CBE,∠ADC=∠BEC,AC=BC,∴△ADC≌△CEB(AAS),∴AD=CE,CD=BE,∴DE=EC﹣CD=AD﹣BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
(1)求证:四边形BDEF为平行四边形;
(2)当∠C=45°,BD=2时,求D,F两点间的距离.

-
科目: 来源: 题型:
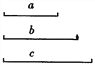
查看答案和解析>>【题目】作图题: (1)已知:如图,线段a、b、c.
求作:ΔABC,使得BC=a,AC=b,AB=c.(保留作图痕迹,不写作法)
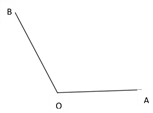
(2)求作:∠AOB的平分线OC.(不写作法,保留作图痕迹)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于圆O,∠BAD=90°,AC为直径,过点A作圆O的切线交CB的延长线于点E,过AC的三等分点F(靠近点C)作CE的平行线交AB于点G,连结CG.
(1)求证:AB=CD;
(2)求证:CD2=BEBC;
(3)当CG=
 ,BE=
,BE= 时,求CD的长.
时,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这
个分式为“和谐分式”.
(1)下列分式:①
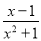 ;②
;②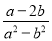 ;③
;③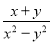 ;④
;④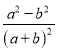 . 其中是“和谐分式”是 (填写序号即可);
. 其中是“和谐分式”是 (填写序号即可);(2)若
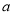 为正整数,且
为正整数,且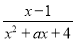 为“和谐分式”,请写出
为“和谐分式”,请写出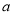 的值;
的值;(3)在化简
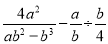 时,
时,小东和小强分别进行了如下三步变形:
小东:
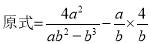
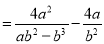
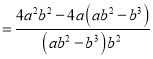
小强:
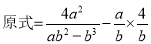
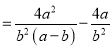
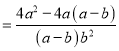
显然,小强利用了其中的和谐分式, 第三步所得结果比小东的结果简单,
原因是: ,
请你接着小强的方法完成化简.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明放学回家后,问爸爸、妈妈小牛队与太阳队篮球比赛结果。下面是他与他父母亲的对话.
小明:“爸爸妈妈,小牛队与太阳队篮球比赛结果如何?”
爸爸:“本场比赛太阳队的纳什比小牛队的特里多得了12分。”
妈妈:“特里得分的2倍与纳什得分的差大于10,纳什得分的2倍比特里得分的3倍还多。”
爸爸又说:“如果特里得分超过20分,则小牛队赢,否则太阳队赢”
请你帮小明分析一下,究竟是哪个队赢了。本场比赛特里、纳什各得了多少分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的有( )
①由两条射线所组成的图形叫做角;
②两点之间,线段最短:
③两个数比较大小,绝对值大的反而小:
④单项式和多项式都是整式.
A.1个B.2个C.3个D.4个
相关试题

