【题目】如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
(1)求证:四边形BDEF为平行四边形;
(2)当∠C=45°,BD=2时,求D,F两点间的距离.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)由等腰三角形的性质得出∠ABC=∠C,证出∠AEG=∠ABC=∠C,四边形CDEG是平行四边形,得出∠DEG=∠C,证出∠F=∠DEG,得出BF∥DE,即可得出结论;
(2)证出△BDE、△BEF是等腰直角三角形,由勾股定理得出BF的值,作FM⊥BD于M,连接DF,则△BFM是等腰直角三角形,由勾股定理得出FM的值,进而得出DM=3,在Rt△DFM中,由勾股定理求出DF即可.
试题解析:(1)证明:∵△ABC是等腰三角形,∴∠ABC=∠C,∵EG∥BC,DE∥AC,∴∠AEG=∠ABC=∠C,四边形CDEG是平行四边形,∴∠DEG=∠C,∵BE=BF,∴∠BFE=∠BEF=∠AEG=∠ABC,∴∠F=∠DEG,∴BF∥DE,∴四边形BDEF为平行四边形;
(2)解:∵∠C=45°,∴∠ABC=∠BFE=∠BEF=45°,∴△BDE、△BEF是等腰直角三角形,∴BF=BE=![]() BD=
BD=![]() ,作FM⊥BD于M,连接DF,如图所示:
,作FM⊥BD于M,连接DF,如图所示:

则△BFM是等腰直角三角形,∴FM=BM=![]() BF=1,∴DM=3,在Rt△DFM中,由勾股定理得:DF=
BF=1,∴DM=3,在Rt△DFM中,由勾股定理得:DF=![]() =
=![]() ,即D,F两点间的距离为
,即D,F两点间的距离为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的菱形ABCD中,BD=4,E、F分别是AD、CD上的动点(包含端点),且AE+CF=4,连接BE、EF、FB.
(1)试探究BE与BF的数量关系,并证明你的结论;
(2)求EF的最大值与最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:式子x﹣2的值为6,则式子3x﹣6的值为( )
A.9B.12C.18D.24
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c是△ABC的三边,满足
 ,且a+b+c=12.
,且a+b+c=12.(1)试求a,b,c的值;
(2)试求△ABC的面积.
-
科目: 来源: 题型:
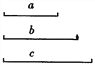
查看答案和解析>>【题目】作图题: (1)已知:如图,线段a、b、c.
求作:ΔABC,使得BC=a,AC=b,AB=c.(保留作图痕迹,不写作法)
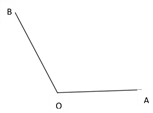
(2)求作:∠AOB的平分线OC.(不写作法,保留作图痕迹)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于圆O,∠BAD=90°,AC为直径,过点A作圆O的切线交CB的延长线于点E,过AC的三等分点F(靠近点C)作CE的平行线交AB于点G,连结CG.
(1)求证:AB=CD;
(2)求证:CD2=BEBC;
(3)当CG=
 ,BE=
,BE= 时,求CD的长.
时,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.在△ABC中,
 ,
, ,直线
,直线 经过点
经过点 ,且
,且 于
于 ,
,  于
于 .
.(1)当直线
 绕点
绕点 旋转到图1的位置时,
旋转到图1的位置时,  的数量关系是_________________ ,并请给出证明过程.
的数量关系是_________________ ,并请给出证明过程.(2)当直线
 绕点
绕点 旋转到图2的位置时,
旋转到图2的位置时,  的数量关系是_________________ (直接写出结果)。
的数量关系是_________________ (直接写出结果)。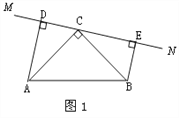

相关试题

