【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )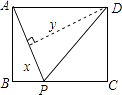
A.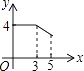
B.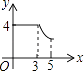
C.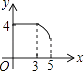
D.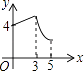
参考答案:
【答案】B
【解析】解:①点P在AB上时,0≤x≤3,点D到AP的距离为AD的长度,是定值4;②点P在BC上时,3<x≤5,
∵∠APB+∠BAP=90°,
∠PAD+∠BAP=90°,
∴∠APB=∠PAD,
又∵∠B=∠DEA=90°,
∴△ABP∽△DEA,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴y= ![]() ,
,
纵观各选项,只有B选项图形符合.
故选:B.
①点P在AB上时,点D到AP的距离为AD的长度,②点P在BC上时,根据同角的余角相等求出∠APB=∠PAD,再利用相似三角形的对应边成比例的性质列出比例式整理得到y与x的关系式,从而得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中, △ABC三个顶点的位置如图(每个小正方形的边长均为1).
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向下平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
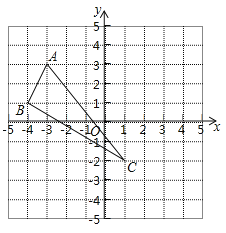
(2)直接写出A′、B′、C′三点的坐标:
A′(_____,______); B′(_____,______);
C′(_____,______).
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.

(1)求抛物线的解析式;
(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )
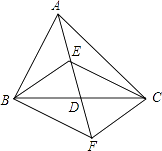
A.BE⊥CE
B.BF∥CE
C.BE=CF
D.AB=AC -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
,  ,
,  ,试说明:BE∥CF.
,试说明:BE∥CF.完善下面的解答过程,并填写理由或数学式:
解:∵
 (已知)
(已知)∴AE∥ ( )
∴
 ( )
( )∵
 (已知)
(已知)∴
 ( )
( )∴DC∥AB( )
∴
 ( )
( )即

∵
 (已知)
(已知)∴
 ( )
( )即

∴BE∥CF( ) .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
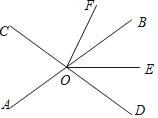
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
(3)若|∠AOC﹣∠BOF|=α°,请直接写出∠AOC和∠BOF的度数.(用含的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2015次运动后,动点P的坐标是( )
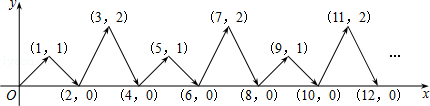
A.(2015,0)
B.(2015,1)
C.(2015,2)
D.(2016,0)
相关试题

