【题目】如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
(1)求抛物线的解析式;
(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:由y=ax2+bx﹣3得C(0.﹣3),
∴OC=3,
∵OC=3OB,
∴OB=1,
∴B(﹣1,0),
把A(2,﹣3),B(﹣1,0)代入y=ax2+bx﹣3得 ![]() ,
,
∴ ![]() ,
,
∴抛物线的解析式为y=x2﹣2x﹣3
(2)
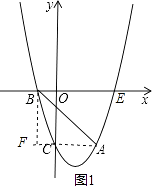
解:设连接AC,作BF⊥AC交AC的延长线于F,
∵A(2,﹣3),C(0,﹣3),
∴AF∥x轴,
∴F(﹣1,﹣3),
∴BF=3,AF=3,
∴∠BAC=45°,
设D(0,m),则OD=|m|,
∵∠BDO=∠BAC,
∴∠BDO=45°,
∴OD=OB=1,
∴|m|=1,
∴m=±1,
∴D1(0,1),D2(0,﹣1)
(3)
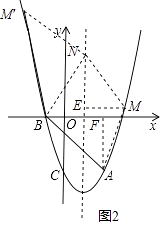
解:设M(a,a2﹣2a﹣3),N(1,n),
①以AB为边,则AB∥MN,AB=MN,如图2,过M作ME⊥对称轴y于E,AF⊥x轴于F,
则△ABF≌△NME,
∴NE=AF=3,ME=BF=3,
∴|a﹣1|=3,
∴a=3或a=﹣2,
∴M(4,5)或(﹣2,11);
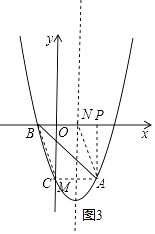
②以AB为对角线,BN=AM,BN∥AM,如图3,
则N在x轴上,M与C重合,
∴M(0,﹣3),
综上所述,存在以点A,B,M,N为顶点的四边形是平行四边形,M(4,5)或(﹣2,11)或(0,﹣3).
【解析】(1)待定系数法即可得到结论;(2)连接AC,作BF⊥AC交AC的延长线于F,根据已知条件得到AF∥x轴,得到F(﹣1,﹣3),设D(0,m),则OD=|m|即可得到结论;(3)设M(a,a2﹣2a﹣3),N(1,n),①以AB为边,则AB∥MN,AB=MN,如图2,过M作ME⊥对称轴y于E,AF⊥x轴于F,于是得到△ABF≌△NME,证得NE=AF=3,ME=BF=3,得到M(4,5)或(﹣2,11);②以AB为对角线,BN=AM,BN∥AM,如图3,则N在x轴上,M与C重合,于是得到结论.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DBE中,BC=BE,还需要添加两个条件才能使△ABC≌△DBE,则不能添加的一组条件是( )
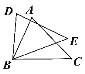
A. AC=DE,∠C=∠E B. BD=AB,AC=DE C. AB=DB,∠A=∠D D. ∠C=∠E,∠A=∠D
-
科目: 来源: 题型:
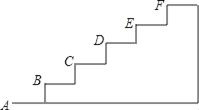
查看答案和解析>>【题目】如图是某台阶的一部分,如果A点的坐标为(0,0),B点的坐标为(1,1),
(1)请建立适当的直角坐标系,并写出其余各点的坐标;
(2)如果台阶有10级,请你求出该台阶的长度和高度;
(3)若这10级台阶的宽度都是2m,单位长度为1m,现要将这些台阶铺上地毯,需要多少平方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中, △ABC三个顶点的位置如图(每个小正方形的边长均为1).
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向下平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
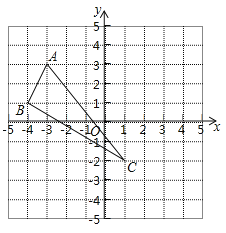
(2)直接写出A′、B′、C′三点的坐标:
A′(_____,______); B′(_____,______);
C′(_____,______).
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )
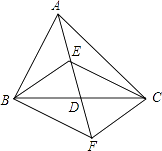
A.BE⊥CE
B.BF∥CE
C.BE=CF
D.AB=AC -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
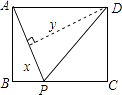
A.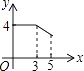
B.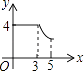
C.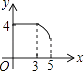
D.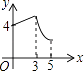
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
,  ,
,  ,试说明:BE∥CF.
,试说明:BE∥CF.完善下面的解答过程,并填写理由或数学式:
解:∵
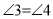 (已知)
(已知)∴AE∥ ( )
∴
 ( )
( )∵
 (已知)
(已知)∴
 ( )
( )∴DC∥AB( )
∴
 ( )
( )即

∵
 (已知)
(已知)∴
 ( )
( )即

∴BE∥CF( ) .

相关试题

